13  Thin-Walled Pressure Vessels

Learning Objectives

• Define thin-walled pressure vessels
• Describe the stresses that exist in thin-walled pressure vessels
• Calculate the stresses generated in the walls of thin-walled pressure vessels
• Perform stress transformation on these stresses

Introduction

Click to expand

Pressure vessels are storage tanks that are used for storing fluids at high pressure and they must be designed to resist this pressure. They are commonly found in factories, power plants, vehicles, and even your own home. Figure 13.1 shows some common applications.

Figure 13.1: Some common examples of pressure vessels. (A) standard home water heater; (B) industrial compressed gas storage; (C) propellant tank for aerospace applications; (D) butane tank for home use.

Pressure vessels are necessarily hollow, and a thin-walled pressure vessel is one where the ratio:

\[ \frac{\text { Inner radius }}{\text { Wall thickness }}>10 \]

This implies that the wall thickness is relatively small compared to the vessel radius. This simplifies our analysis in two ways:

1. We can assume that stresses in the vessel walls are uniform across the thickness of the wall
2. We can ignore stress in the radial direction (perpendicular to the vessel wall)

As we’ll see in this chapter, stresses are generated in the walls of thin-walled pressure vessels in two directions known as the axial stress and hoop stress (Figure 13.2). There is a 3^rd stress in the radial direction but this is very small compared to the other stresses and is assumed to be zero in this text.

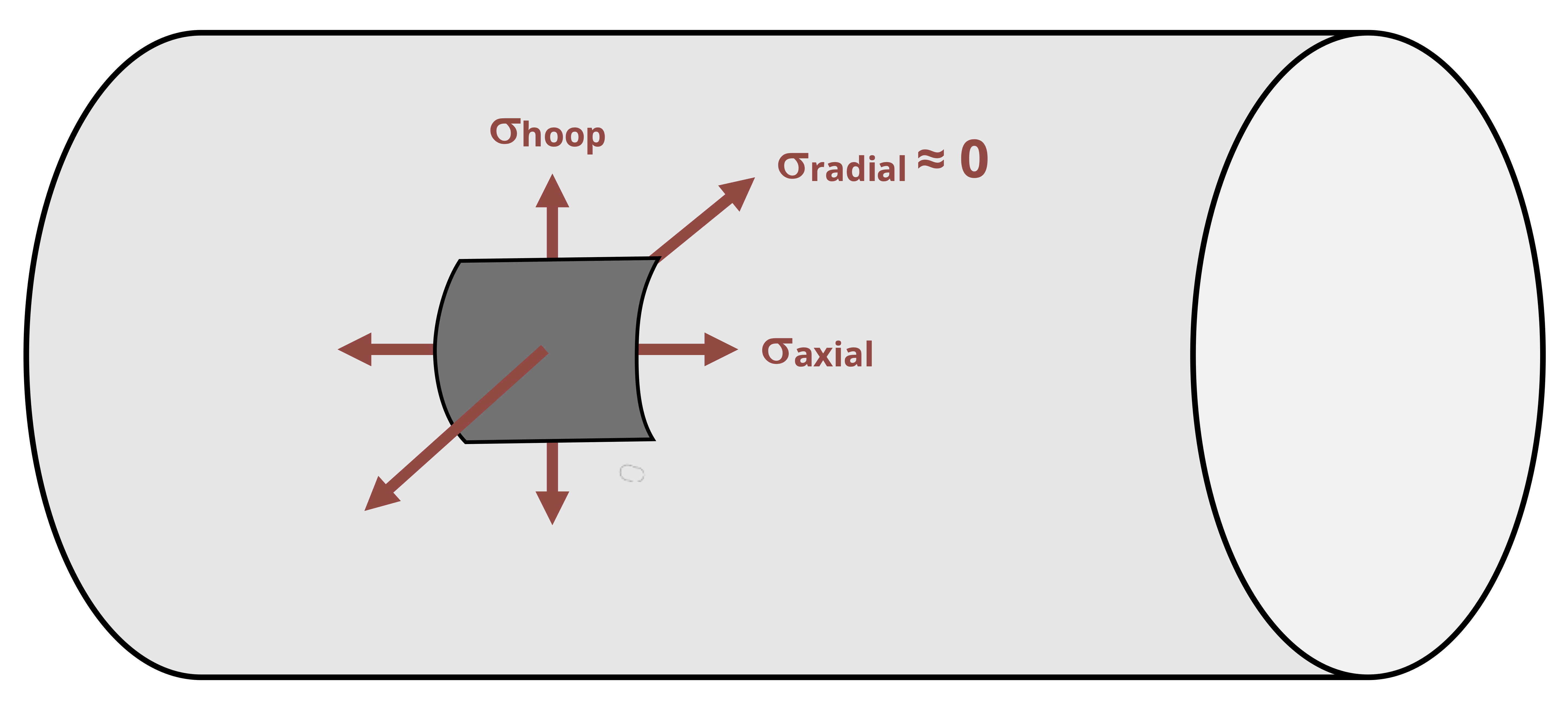
Figure 13.2: A stress element on the wall of a thin-walled pressure vessel. Stresses exist in the axial and hoop directions. The radial stress is very small in comparison and is assumed to be zero.

As seen in Figure 13.1, thin-walled pressure vessels are commonly either cylindrical or spherical. Section 13.1 will discuss the stresses in cylindrical vessels. Section 13.2 will discuss the stresses in spherical vessels.

13.1 Cylindrical Pressure Vessels

Click to expand

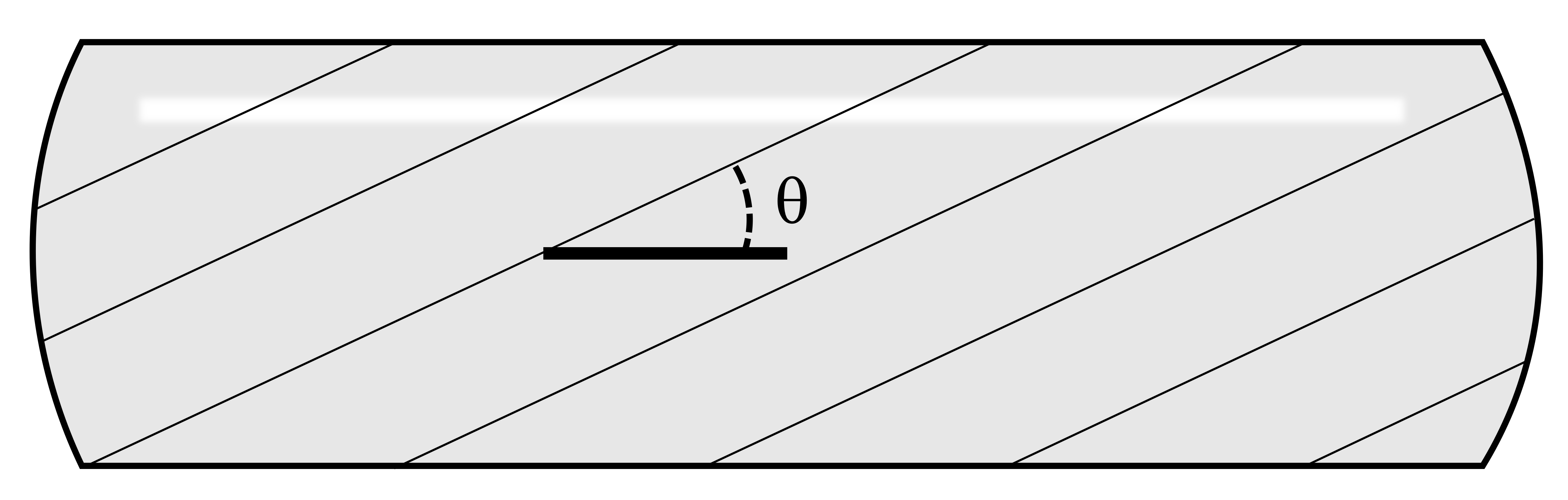
The equations stresses in the wall of a cylindrical pressure vessel can be derived with the help of a free body diagram. Let’s cut a cross-section through our vessel to expose the fluid inside (Figure 13.3).

Figure 13.3: Cross-section through the cylindrical vessel showing the axial stress in the walls (𝜎𝐴) and the fluid pressure P.

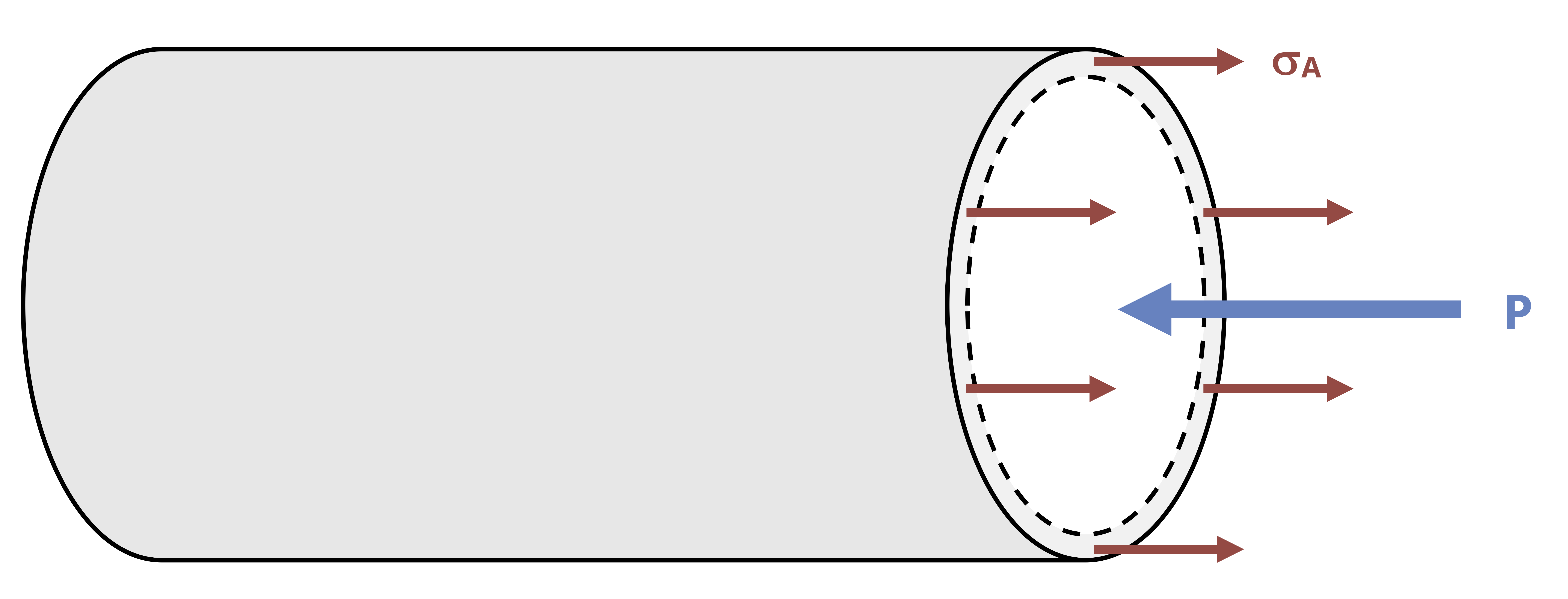
There will be an axial stress from the internal fluid pressure (P) and an axial stress in the walls of the vessel (𝜎_𝐴). Since \(\text{stress}=\frac{\text { force }}{\text { area }}\) we can determine the two forces. The fluid pressure acts over a circular area \(A=\pi r_i^2\). The stress in the walls acts over an area equal to the circumference of the vessel multiplied by the wall thickness, \(A=2 \pi r_i t\).

By equilibrium:

\[ \sum F_x=\left(\sigma_A\right)\left(2 \pi r_i t\right)-(P)\left(\pi r_i^2\right)=0 \\ \]

\[ \boxed{\sigma_A=\frac{P r_i}{2 t}} \tag{13.1}\]

where
𝜎𝐴 = Axial stress in the wall of the vessel [Pa, psi]
P = Fluid pressure inside the vessel [Pa, psi]
ri = Inner radius of the vessel [m, in.]

t = Wall thickness of the vessel [m, in.]

Similarly there will be a stress in the lateral direction, referred to as the hoop stress 𝜎_H. Let’s cut a vertical cross-section (Figure 13.4) to derive an equation for this stress.

Figure 13.4: Cross-section through the cylindrical vessel showing the hoop stress in the walls (𝜎_H) and the fluid pressure P.

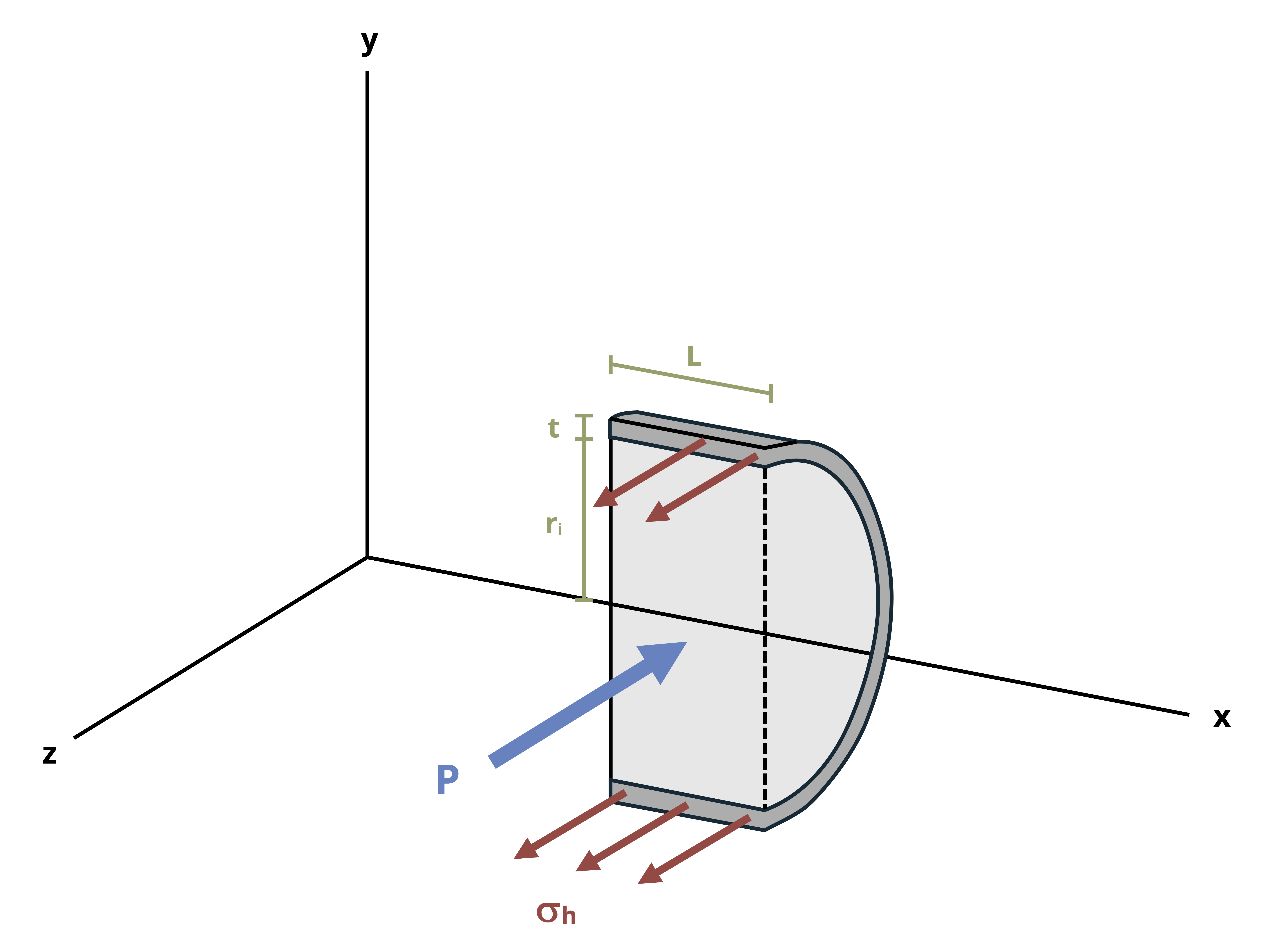
There will again be a stress from the internal fluid pressure (P) and a stress in the walls of the vessel (𝜎_H). The fluid pressure acts over an area of \(A=2 r_i L\). The stress in the walls acts over an area of \(A=2 t L\).

By equilibrium:

\[ \sum F_x=\left(\sigma_H\right)(2 t L)-(P)\left(2 r_i L\right)=0 \\ \]

\[ \boxed{\sigma_H=\frac{P r_i}{t}} \tag{13.2}\]

where
𝜎_H = Hoop stress in the wall of the vessel [Pa, psi]
P = Fluid pressure inside the vessel [Pa, psi]
r_i = Inner radius of the vessel [m, in.]

t = Wall thickness of the vessel [m, in.]

The internal pressure P is typically reported as the gage pressure, which is defined as the internal pressure minus the atmospheric pressure. This allows us to calculate the stresses directly without needing to account for atmospheric pressure.

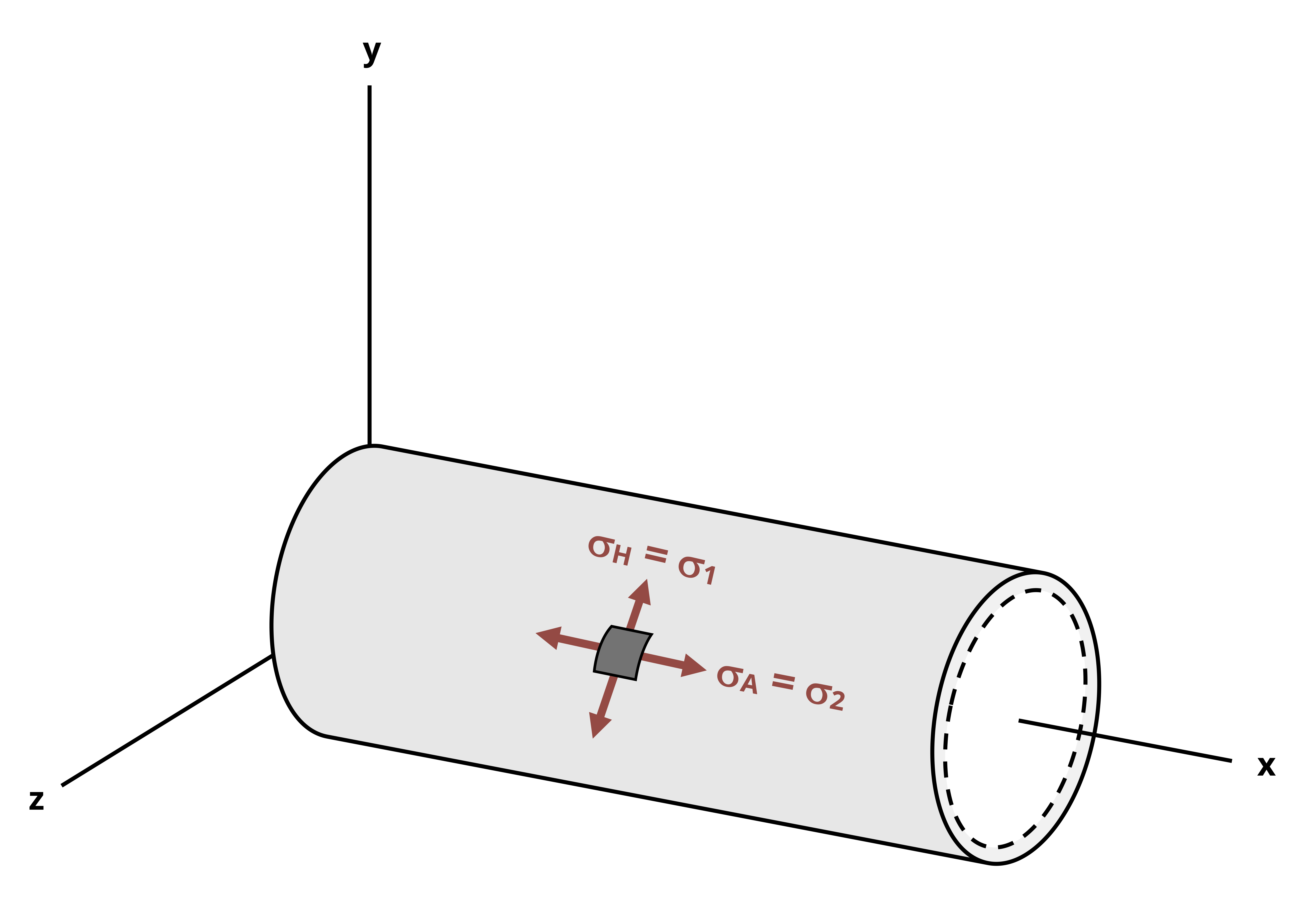
Since the radial stress is assumed to be zero, the axial and hoop stresses represent a state of plane stress such as those discussed in Chapter 12. Further, since there is no shear stress, the axial and hoop stresses represent the principal stresses. Since the hoop stress is larger, this is the first principal stress (𝜎₁). The axial stress is the second principal stress (𝜎₂). The third principal stress acts in the radial direction and has already been assumed to be zero. Figure 13.5 shows a plane stress element representing the stresses in the wall of a cylindrical thin-walled pressure vessel.

Figure 13.5: The hoop stress represents the first principal stress 𝜎₁. The axial stress represents the second principal stress 𝜎₂. There is no shear stress.

By the methods of Chapter 12 we may perform stress transformation on these stresses. Figure 13.6 shows Mohr’s Circle for the in-plane and out-of-plane stresses.

Figure 13.6: Mohr’s Circle for the stresses in the walls of a cylindrical thin-walled pressure vessel, showing principal stresses 𝜎₁ and 𝜎₂. The 3rd principal stress 𝜎₃ = 0.

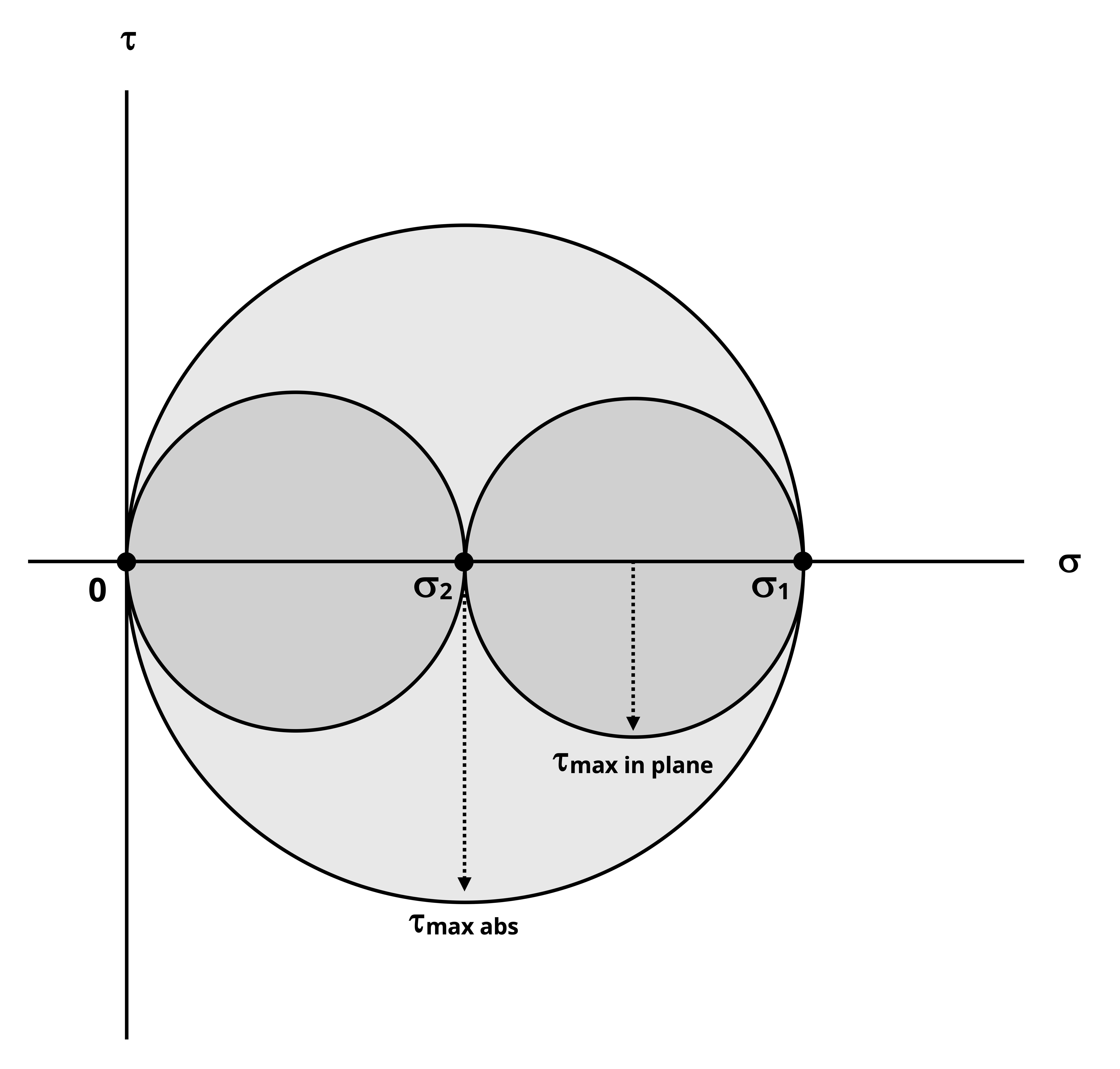
Since the two principal stresses are positive and the third principal stress is zero it should be apparent that the maximum in plane shear stress can be determined as:

\[ \tau_{max~in~plane}=\frac{\sigma_1-\sigma_2}{2} \]

It should also be apparent that the maximum out-of-plane shear stress will be larger and can be calculated from:

\[ \tau_{\max a b s}=\frac{\sigma_1}{2} \]

Example 13.1 demonstrates calculation of the principal stresses and maximum in-plane shear stress for a cylindrical thin-walled pressure vessel. Example 13.2 combine the content from this section with stress transformation from Chapter 12 in order to find the stresses at specific orientations.

Example 13.1

Example 13.1  

A cylindrical pressure vessel has an outer diameter of 8 ft and a wall thickness of 2 inches. The vessel contains propane at a gage pressure of 250 psi. Determine the principal stresses and maximum in-plane shear stress in the walls of the vessel.

Solution

First determine the inner radius of the vessel. It will be easiest to convert this to inches since the other length units in the problem are given in inches.

Outer radius, \(r_o = \frac{8{~ft}}{2} = 4 {~ft} = 48{~in.}\)

Inner radius, \(r_i = 48{~in.} - 2{~in.} = 46{~in.}\)

Now calculate the axial and hoop stresses.

\[ \begin{aligned} & \sigma_A=\frac{Pr_i}{2t}=\frac{250{~psi} * 46{~in.}}{2 * 2{~in.}}=2,875{~psi} \\ & \sigma_H=\frac{Pr_i}{t}=\frac{250{~psi} * 46{~in.}}{2{~in.}}=5,750{~psi} \end{aligned} \]

Since there is no shear stress, these are the principal stresses.

\[ \begin{aligned} & \sigma_1=5,750{~psi} \\ & \sigma_2=2,875{~psi} \end{aligned} \]

Finally, the maximum in-plane shear stress can be found from:

\[ \tau_{max~in~plane}=\frac{\sigma_1-\sigma_2}{2}=\frac{5,750{~psi}-2,875{~psi}}{2}=1,438{~psi} \]

Example 13.2

Example 13.2  

A cylindrical pressure vessel is made by welding steel plate at an angle of 𝜃=25° as shown. The vessel has an outer diameter of 1.5 m and a wall thickness of 40 mm. The vessel contains fluid at a gage pressure of 5 MPa. Determine the normal stress perpendicular to the weld and the shear stress parallel to the weld.

Solution

First determine the inner radius of the vessel. Wall thickness 𝑡 = 40 𝑚𝑚 = 0.04 𝑚.

Outer radius, \(r_o = \frac{1.5{~m}}{2} =0.75{~m}\)

Inner radius, \(r_i = 0.75{~m} - 0.04{~m} = 0.71{~m}\)

Now calculate the axial and hoop stresses.

\[ \begin{aligned} & \sigma_A=\frac{Pr_i}{2t}=\frac{5{~MPa} * 0.71{~m}}{2 * 0.04{~m}}=44.4{~MPa} \\ & \sigma_H=\frac{Pr_i}{t}=\frac{5{~MPa} * 0.71{`m}}{0.04{~m}}=88.8{~MPa} \end{aligned} \]

By the methods of Section 12.1 we can calculate the normal stress perpendicular to the weld. Draw a stress element of a point on the pressure vessel. The axial stress will act horizontally and the hoop stress vertically for this element.

The weld is at an angle of 25° measured counter-clockwise from horizontal. The normal stress perpendicular to this weld is therefore at an angle of 65° clockwise from horizontal. We can determine the normal stress at this orientation from:

\[ \begin{gathered} \sigma_x^{\prime}=\frac{\sigma_x+\sigma_y}{2}+\frac{\sigma_x-\sigma_y}{2} \cos (2 \theta)+\tau_{x y} \sin (2 \theta) \\ \sigma_x^{\prime}=\frac{44.4{~MPa}+88.8{~MPa}}{2}+\frac{44.4{~MPa}-88.8{~MPa}}{2} \cos \left(2 *-65^{\circ}\right)+0 \\ \sigma_x^{\prime}=66.6{~MPa}-22.2{~MPa}*\cos \left(-130^{\circ}\right) \\ \sigma_x^{\prime}=80.9{~MPa} \end{gathered} \]

The shear stress occurs parallel to the weld at an angle of 25° counter-clockwise from the horizontal. We can determine the shear stress at this orientation from:

\[ \begin{gathered} \tau_{x^{\prime} y^{\prime}}=-\left(\frac{\sigma_x-\sigma_y}{2}\right) \sin (2 \theta)+\tau_{x y} \cos (2 \theta) \\ \tau_{x^{\prime} y^{\prime}}=-\left(\frac{44.4{~MPa}-88.8{~MPa}}{2}\right) \sin \left(2 * 25^{\circ}\right)+0 \\ \tau_{x^{\prime} y^{\prime}}=-\left(\frac{44.4{~MPa}-88.8{~MPa}}{2}\right) \sin \left(2 * 25^{\circ}\right)+0 \\ \tau_{x^{\prime} y^{\prime}}=22.2{~MPa}* \sin \left(50^{\circ}\right) \\ \tau_{x^{\prime} y^{\prime}}=17.0{~MPa} \end{gathered} \]

Step-by-step: Cylindrical thin-walled pressure vessels

1. Determine the inner radius, wall thickness, and internal gage pressure for the vessel

2. Calculate the axial \(\left(\sigma_A=\frac{P r_i}{2 t}\right)\) and hoop \(\left(\sigma_H=\frac{P r_i}{t}\right)\) stresses—these are the principal stresses

3. Perform any stress transformation calculations as required

13.2 Spherical Pressure Vessels

Click to expand

A spherical vessel will yield the same cross-section regardless of the axis it is cut along (Figure 13.7). The stress in the walls of a spherical vessel is the same as the axial stress in a cylindrical vessel.

By equilibrium:

\[ \sum F_x=\left(\sigma_A\right)\left(2 \pi r_i t\right)-(P)\left(\pi r_i^2\right)=0 \]

\[ \boxed{\sigma_A=\frac{P r_i}{2 t}} \tag{13.3}\]

where
𝜎_A = Axial stress in the wall of the vessel [Pa, psi]
P = Fluid pressure inside the vessel [Pa, psi]
r_i = Inner radius of the vessel [m, in.]

t = Wall thickness of the vessel [m, in.]

Figure 13.7: Cross-section through the spherical vessel showing the axial stress in the walls (𝜎_A) and the fluid pressure P.

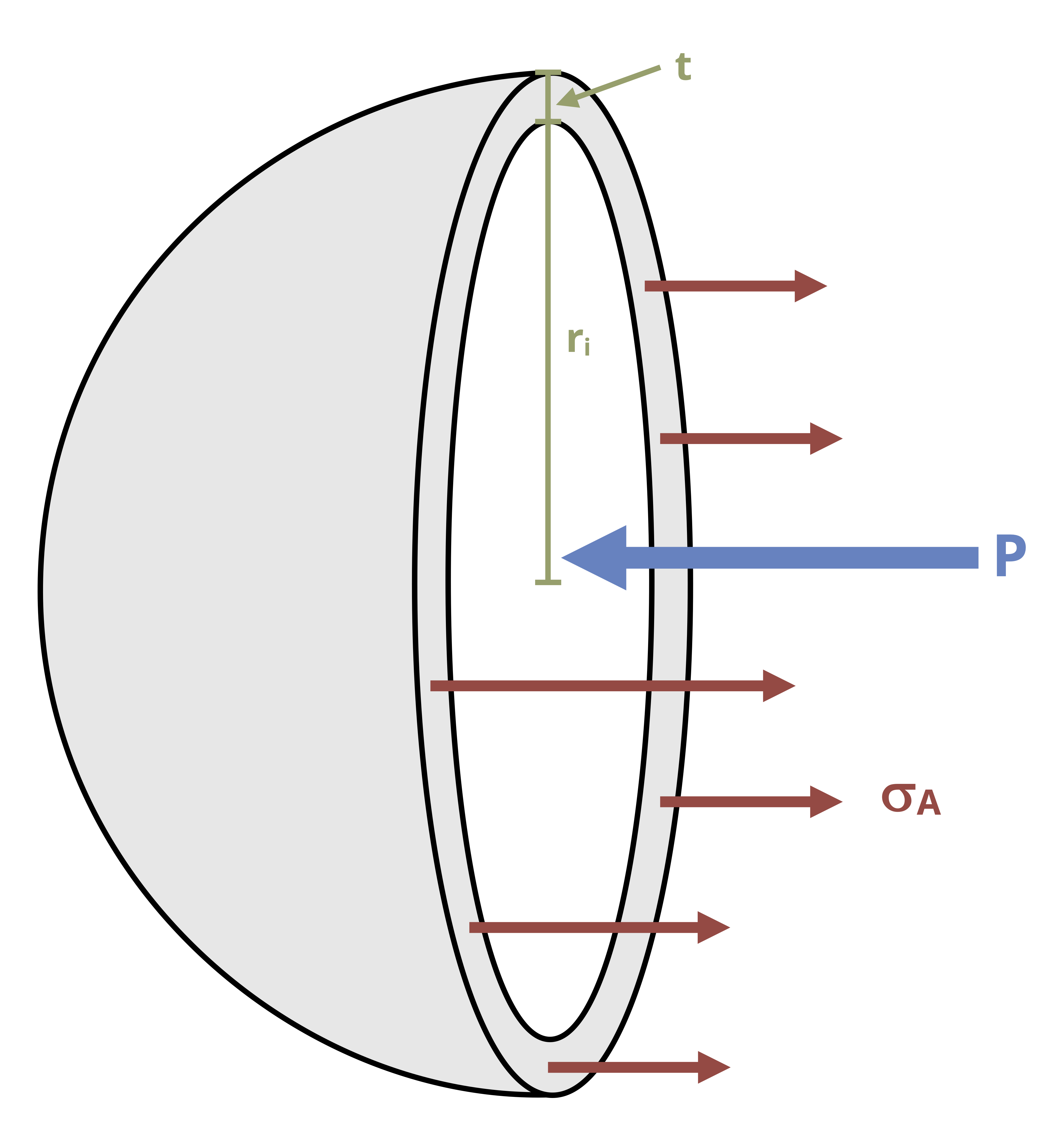
In this case, the same stress exists in both principal directions. We will again assume that the radial stress is zero, meaning that these stresses again form a state of plane stress (Figure 13.8). There is again no shear stress, so these stresses are the principal stresses. In this case, the two principal stresses are the same.

Figure 13.8: Spherical vessels experience the same axial stress in both principal directions. There is no shear stress.

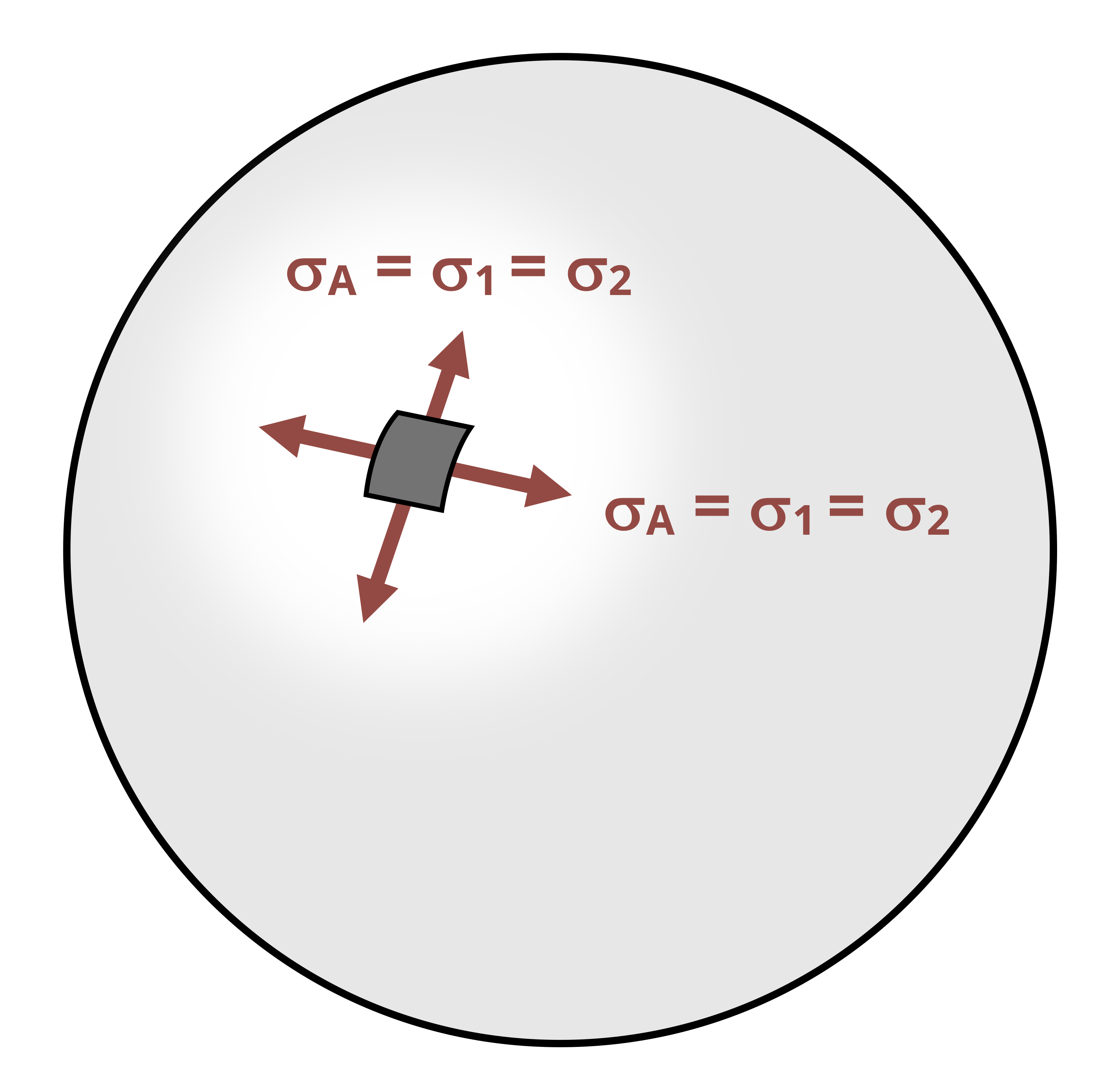
Note that these principal stresses are equal to 𝜎₂ in the cylindrical vessel. As such, spherical vessels are stronger than cylindrical vessels. However, they are also more expensive to manufacture so cylindrical vessels are still very common.

We may again use the methods of Chapter 12 to perform stress transformation. Figure 13.9 shows Mohr’s Circle for the in-plane and out-of-plane stresses.

Figure 13.9: Mohr’s Circle for the stresses in the walls of a spherical thin-walled pressure vessel. Principal stresses 𝜎₁ = 𝜎₂ and the in-plane circle reduces to a single point. The 3rd principal stress 𝜎₃ = 0.

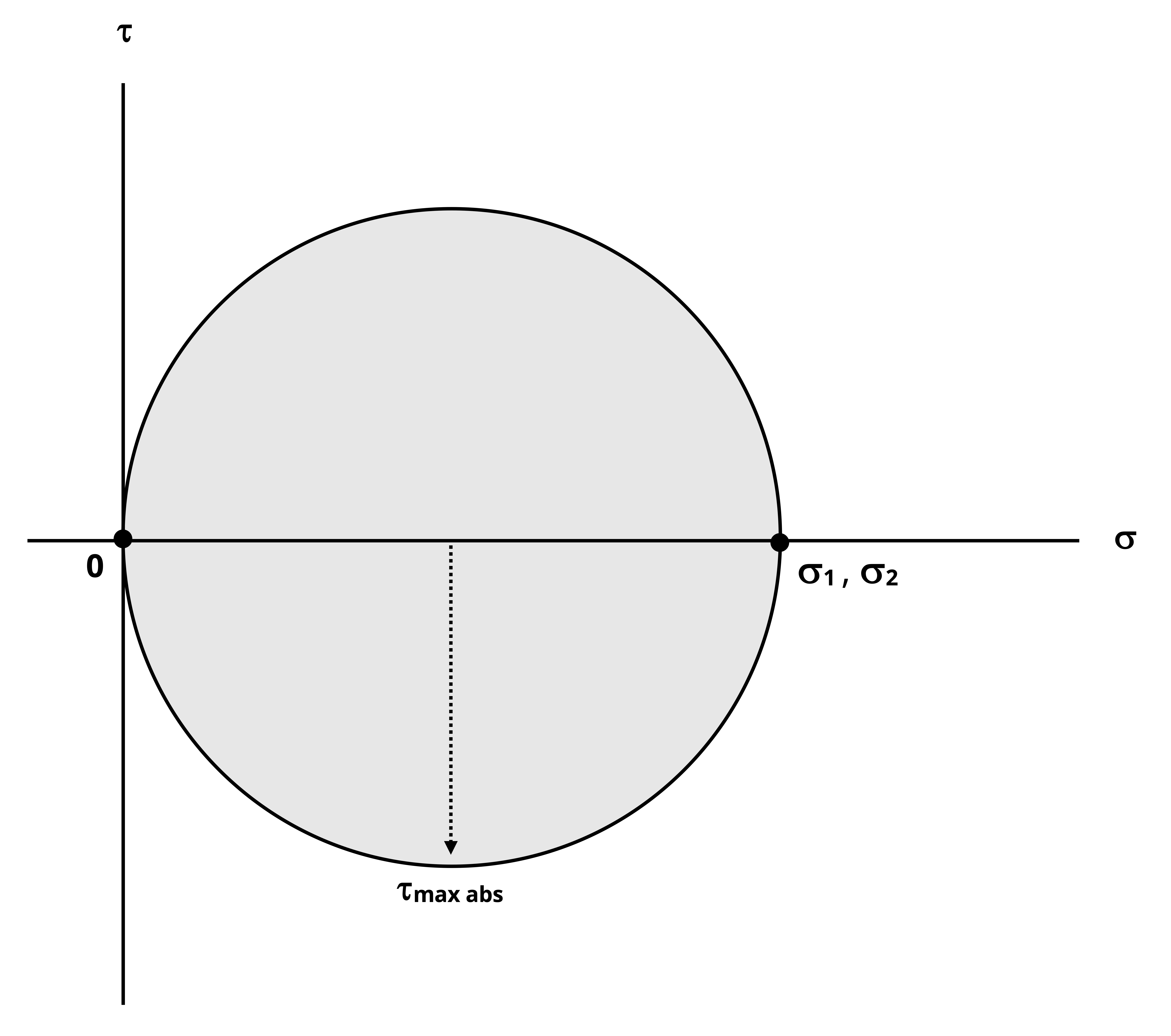
This time 𝜎₁ = 𝜎₂ and so the in-plane Mohr’s Circle reduces to a single point. The maximum in-plane shear stress is therefore zero. The maximum out-of-plane shear stress can be calculated from:

\[ \tau_{\max a b s}=\frac{\sigma_1}{2} \]

Example 13.3 demonstrates the design of a spherical vessel, based on the allowable stress in the vessel walls.

Example 13.3

Example 13.3  

A spherical pressure vessel is made of steel with a yield strength of 250 MPa. The vessel has an outer diameter of 4 meters and a wall thickness of 25 mm. If the factor of safety with respect to yield is 2.5, determine the maximum allowable gage pressure of the fluid within the vessel.

Solution

Wall thickness, \(𝑡 = 25{~𝑚𝑚} = 0.025{~𝑚}\)

Outer radius, \(r_o = 2{~m}\)

Inner radius, \(r_i= 2{~m} - 0.025{~m} = 1.975{~m}\)

Start by using the factor of safety to find the maximum allowable stress in the walls of the vessel.

\[ \sigma_{allow}=\frac{250{~MPa}}{2.5}=100{~MPa} \]

Spherical vessels experience the same stress in both directions:

\[ \sigma_A=\frac{P r_i}{2 t} \]

Rearrange this equation to solve for P:

\[ \begin{gathered} P=\frac{\sigma_A * 2 t}{r_i} \\ \\ P=\frac{100{~MPa}*2*0.025{~m}}{1.975{~m}}=2.53{~MPa} \end{gathered} \]

Step-by-step: Spherical thin-walled pressure vessels

1. Determine the inner radius, wall thickness, and internal gage pressure for the vessel
2. Calculate the axial stress \(\left(\sigma_A=\frac{P r_i}{2 t}\right)\). This stress will be the same in both the horizontal and vertical directions
3. Perform any stress transformation calculations as required

13.3 Summary

Click to expand

Key takeaways

Pressure vessels contain fluids at high pressure. A thin walled pressure vessel is one where \(\frac{\text { Inner radius }}{\text { Wall thickness }}>10\).

For thin walled pressure vessels, the stresses in the vessel walls are assumed to be constant across the thickness of the wall and the stress in the radial direction is assumed to be zero. The stresses created in the axial and hoop directions by the fluid pressure are the principal stresses.

Pressure vessels are commonly cylindrical or spherical. Cylindrical vessels experience both axial and hoop stresses. The axial stress is half of the hoop stress. Spherical vessels experience only an axial stress. As such, spherical vessels experience less stress than cylindrical vessels.

There is no shear stress generated in the axial and hoop directions. However, stress transformation can be used to determine both in-plane and out-of-plane shear stresses.

Key equations

Cylindrical thin-walled pressure vessels

Hoop stress:

\[ \sigma_H=\frac{P r_i}{t}=\sigma_1 \]

Axial stress:

\[ \sigma_A=\frac{P r_i}{2 t}=\sigma_2 \]

Maximum in-plane shear stress:

\[ \tau_{max~in~plane}=\frac{\sigma_1-\sigma_2}{2} \]

Absolute maximum shear stress:

\[ \tau_{\max a b s}=\frac{\sigma_1}{2} \]

Spherical thin-walled pressure vessels

Axial stress:

\[ \sigma_A=\frac{P r_i}{2 t}=\sigma_1=\sigma_2 \]

Absolute maximum shear stress:

\[ \tau_{\max a b s}=\frac{\sigma_1}{2} \]

References

Click to expand

Figures

Figure 13.1: Some common examples of pressure vessels. A: Tomwsulcer. 2013. Public domain. https://commons.wikimedia.org/wiki/File:Hot_water_heater_with_pipe.jpg. B: James Lord. 2024. CC BY-NC-SA. C: NASA. 2009. No known copyright restrictions. https://flic.kr/p/93mnwD.

Figure 13.2: A stress element on the wall of a thin-walled pressure vessel. Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.3: Cross-section through the cylindrical vessel showing the axial stress in the walls (𝜎_𝐴) and the fluid pressure P. Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.4: Cross-section through the cylindrical vessel showing the hoop stress in the walls (𝜎_H) and the fluid pressure P. Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.5: The hoop stress represents the first principal stress 𝜎₁. Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.6: Mohr’s Circle for the stresses in the walls of a cylindrical thin-walled pressure vessel, showing principal stresses 𝜎₁ and 𝜎₂. Kindred Grey. 2024. CC BY-NC-SA.

Example 13.2: Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.7: Cross-section through the spherical vessel showing the axial stress in the walls (𝜎_A) and the fluid pressure P. Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.8: Spherical vessels experience the same axial stress in both principal directions. Kindred Grey. 2024. CC BY-NC-SA.

Figure 13.9: Mohr’s Circle for the stresses in the walls of a spherical thin-walled pressure vessel. Kindred Grey. 2024. CC BY-NC-SA.