14 Combined Loads
Introduction
Click to expand
In this chapter, we will use of all of the previously discussed concepts to determine the total normal stress and the total shear stress for a body subjected to various types of loading simultaneously. Axial forces (Chapter 5), bending moments (Chapter 9), and pressure (Chapter 13) may be applied in various combinations to give total normal stress. Transverse loads (Chapter 10) in multiple directions and torsion (Chapter 6) can combine to give total shear stress.
As part of understanding which loads lead to which types of stresses and in which directions, it will be important to have a good understanding of coordinate axes. In particular, we will want to be able to distinguish between the longitudinal axis and the cross-sectional axes. This can change from body to body as different coordinate axes are used, but it can also change within an individual body based on changes in geometry. In Section 14.1, we will review how to distinguish between the coordinate axes as well as define generic terms that will allow us to express equations in a more generalized manner.
In Section 14.2, the various sources of normal stress are reviewed and expanded on. They will be re-framed in terms of the general axes discussed in @sect-14.1 so as to clarify which other normal stresses they may combine with. In Section 14.2.1 we will revisit bending stress to express the unsymmetric bending stress equation in terms of general cross-sectional axes. In Section 14.2.3, eccentric loading, which is a specific instance of combined normal stress in which normal forces result in bending, will be considered.
In Section 14.3, we will focus on combining the various sources of shear stress to determine the total shear stress. To expand on the concepts discussed and used in Chapter 6 and Chapter 10, we will perform calculations based on both possible transverse loading directions as well as torsion. As in Section 14.2, this will be done with a general set of coordinate axes.
In Section 14.4, we will further expand the above cases to situations in which all combinations of loading are possible and the general stress state is determined.
Note that the determination of internal reactions for the general problems presented in this chapter will require the use of 3D equilibrium equations, particularly for determining bending moments and torsion. You may find it helpful to review Section 1.4 to understand these calculations.
14.1 Coordinate Axes and Directions
Click to expand
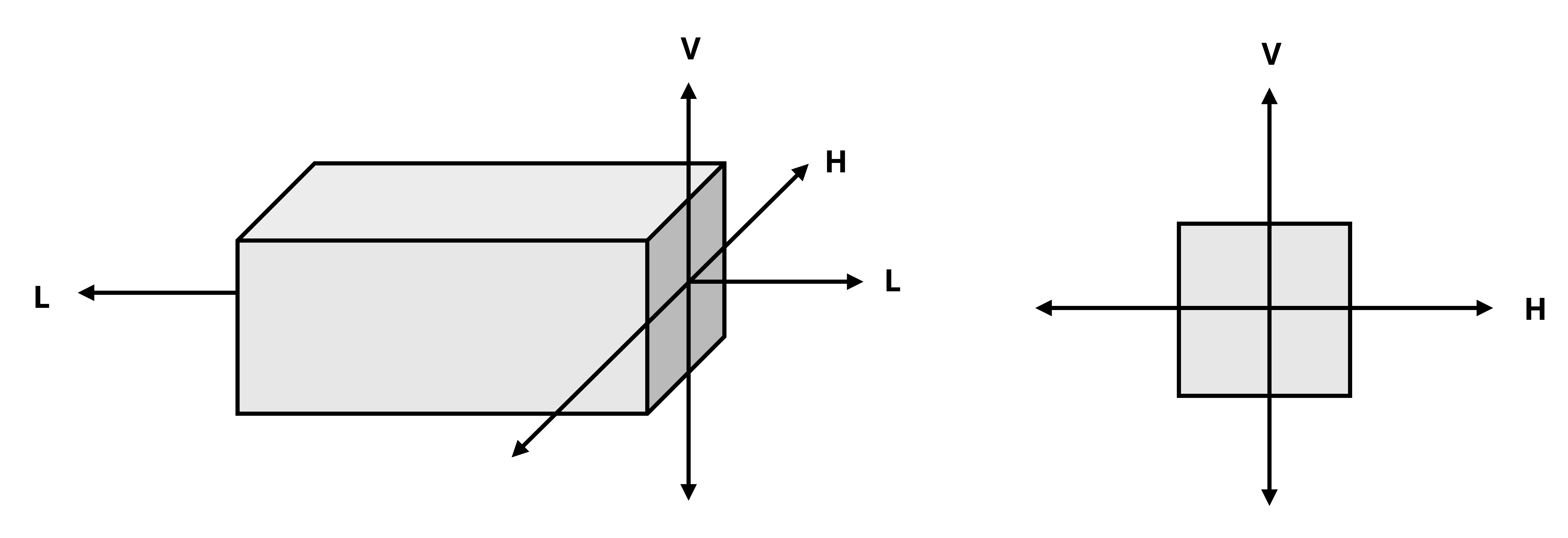
To generalize the discussion for any set of coordinate axes, we will use generic terms for the various directions, as shown in Figure 14.1. The vertical axis of the cross-section will be referred to as the V axis, the horizontal axis of the cross-section will be referred to as the H axis, and the longitudinal (axial) direction will be referred to as the L axis.
The longitudinal direction, synonymous with axial direction, is the direction perpendicular to a cross-section which is cut at a point of interest on a body. The cross-sectional axes are the axes one would draw on the cross-section based on viewing the cross-section down the longitudinal axis.
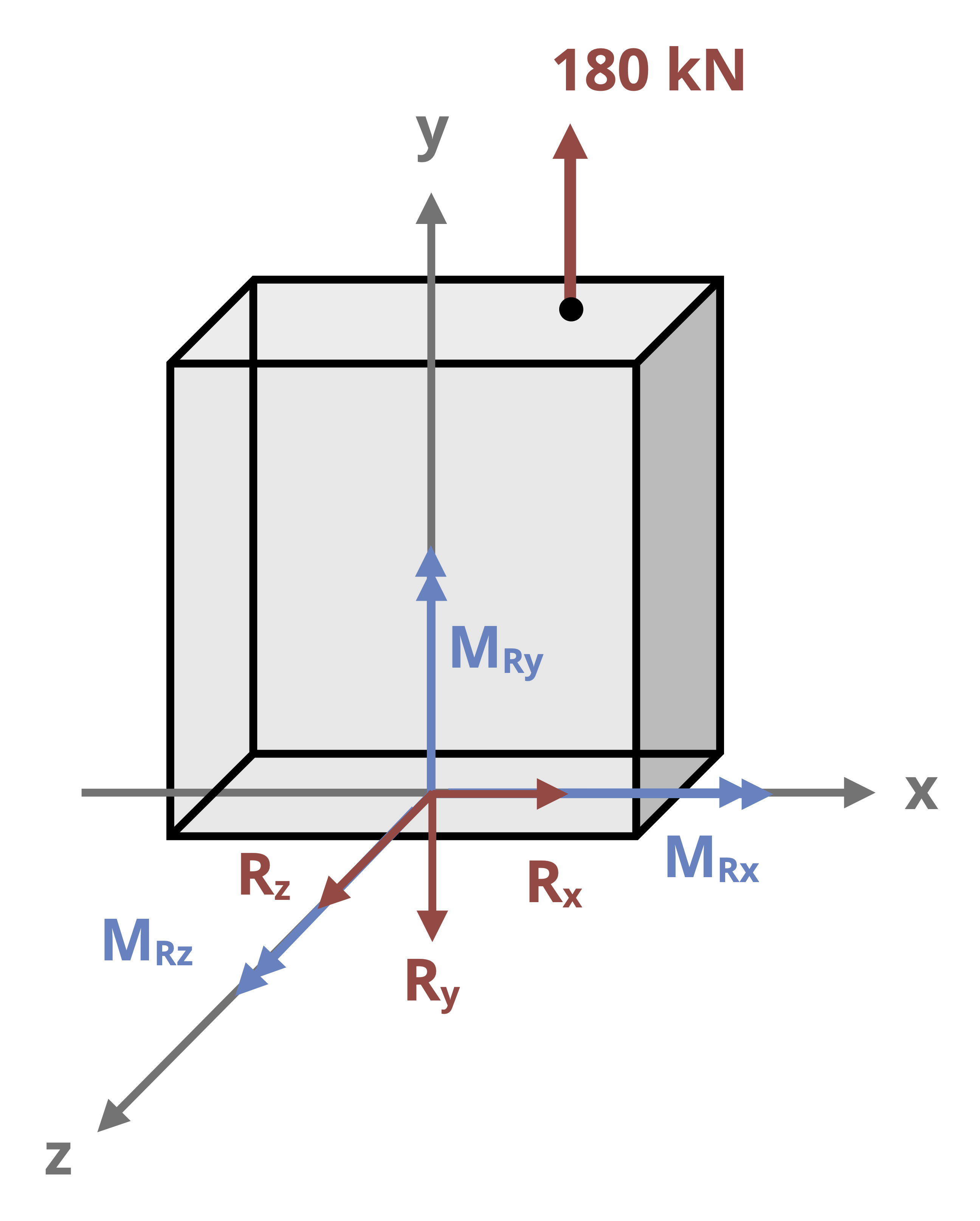
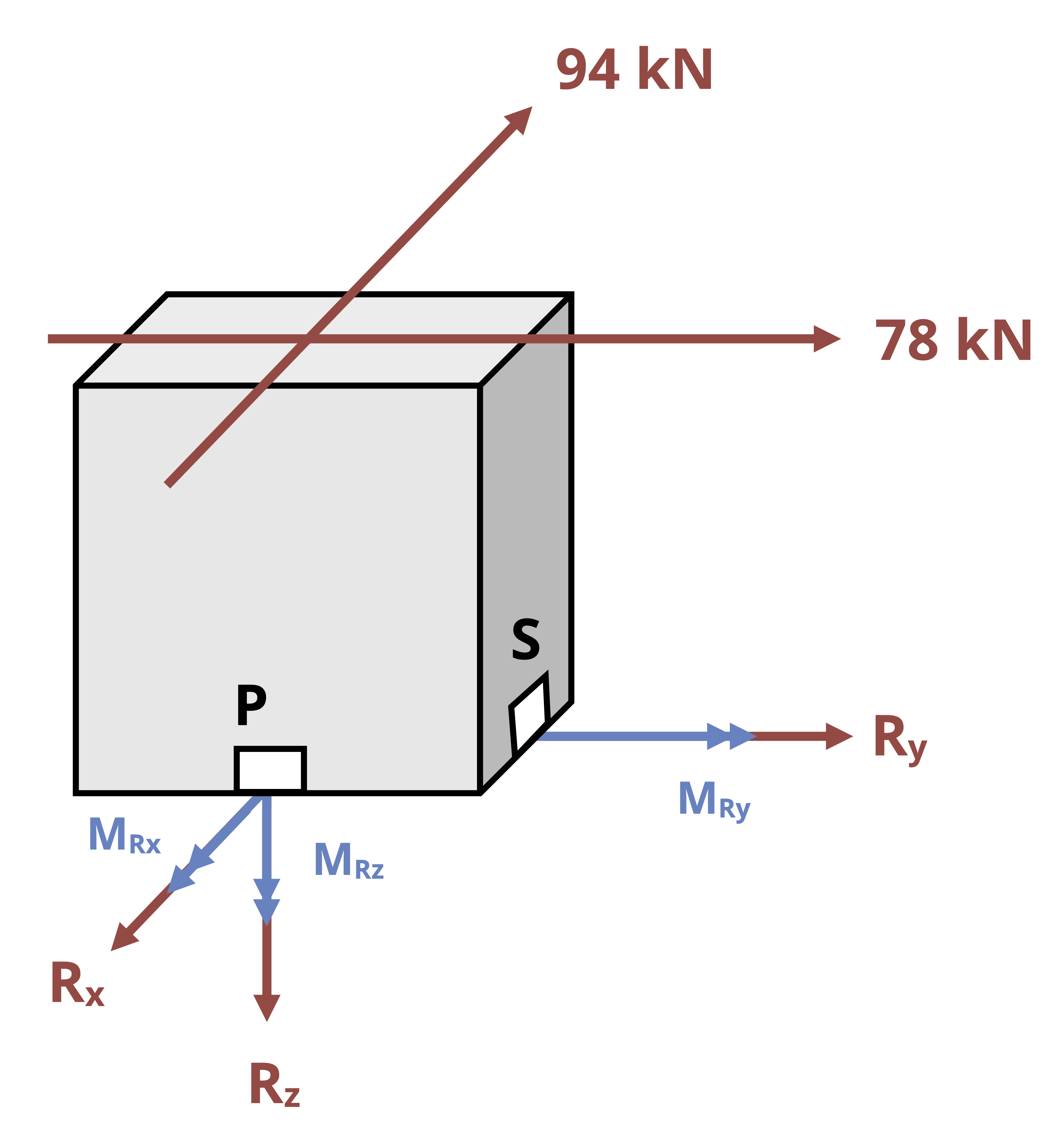
These directions could change from point to point depending on the location of the point and the geometry of the body. For example, consider the structure in Figure 14.2 with the x, y, z axes oriented at the origin as shown. If we want to examine point P on the structure, we make a vertical cut at point P. The direction normal to the cut surface is the x-direction, so the x axis is the longitudinal axis.
When you view the cut surface looking down the x-axis, you see the y and z axes on the cross-section, so those are the cross-sectional axes. In this view, the y axis appears to be the vertical (V) axis of the cross-section the the z axis is horizontal (H).
On the other hand, for point Q, we must make a horizontal cut to examine that point. The normal direction to the cut is then the vertical, or y-axis, and the cross-sectional axes as viewed looking down the y-axis are the x and z axes. In this view, the x axis would appear to be the horizontal axis of the cross-section and the z axis would appear to the vertical axis of the cross-section.
Note that depending on your perspective, you may switch which of the cross-sectional axes you consider to be horizontal versus vertical. Ultimately this will not matter as long as you correctly distinguish between the longitudinal and cross-sectional directions.
In the following sections, we will express equations in terms of these generic directions so that they will apply to any orientation of coordinate axes.
14.2 Combined Normal Stress
Click to expand
In previous chapters, individual sources of longitudinal normal stress were considered: axial loads (@sec-axial-loading), bending loads (Chapter 9), and pressure loads (Chapter 13). With all three of these forms of loading present, we can express the generalized equation for total longitudinal stress as:
\[ \sigma_L =\frac{\sum F_L}{A}+\sigma_{bending}+\frac{p r}{2 t} \]
where:
𝜎L = total normal stress in longitudinal direction {Pa, psi]
FL = force in the longitudinal direction {N, lb]
A = cross-sectional area [m2, in2]
𝜎bending = bending stress (discussed in more detail below) [Pa, psi]
p = internal pressure [Pa, psi]
r = inner radius of pipe or pressure vessel [m, in]
t = wall thickness of pipe or pressure vessel [m, in]
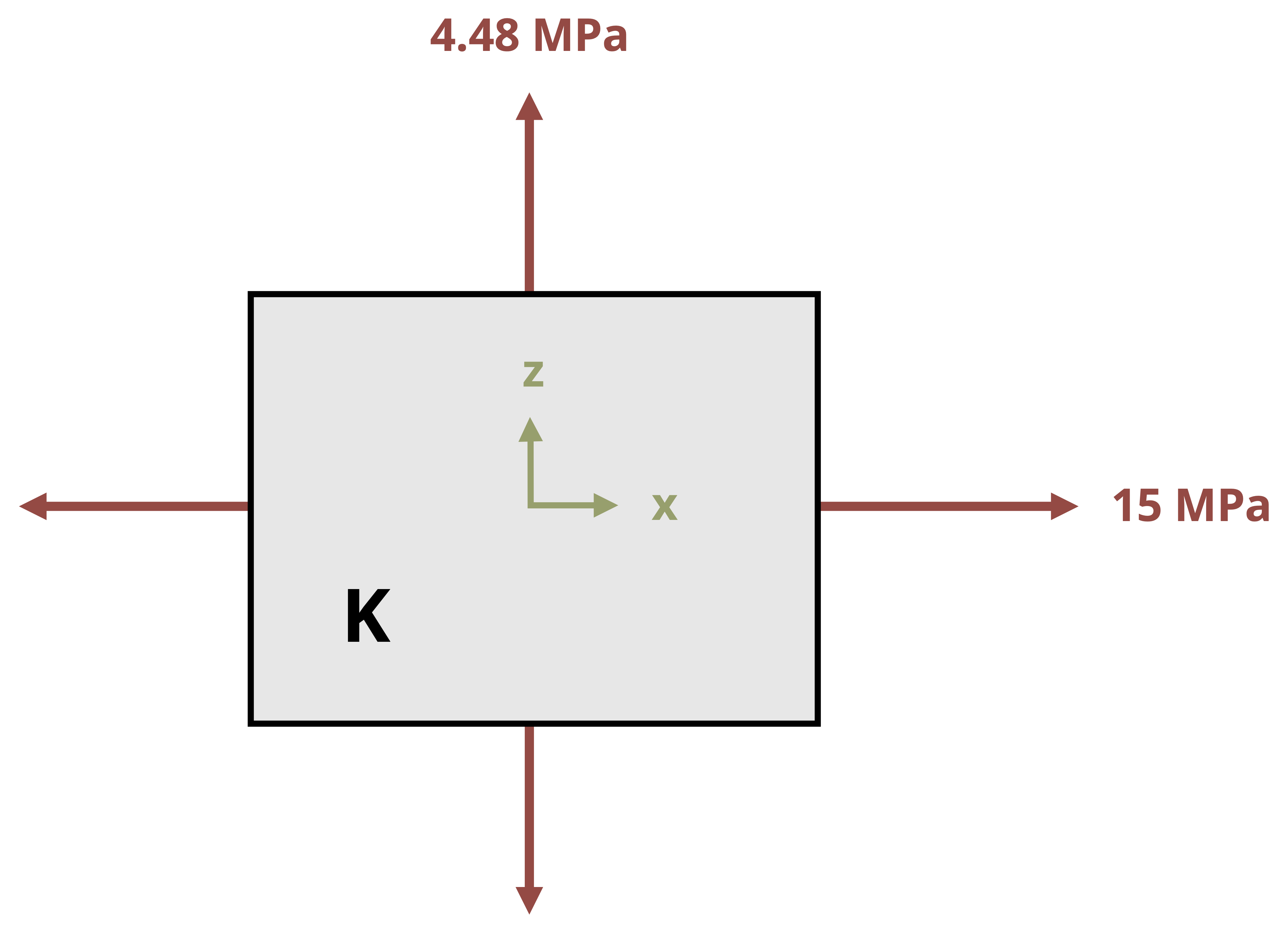
If there is pressure loading, in addition to the contribution to the longitudinal normal stress indicated above, there will also be normal stress in the cross-sectional directions equal to the hoop stress.
\[\sigma_V=\sigma_H=\sigma_{hoop}=\frac{pr} {t}\]
Of course, for problems with no pressure, the pressure terms would be excluded.
Of the three types of longitudinal normal stress, bending stress tends to be the most complex to understand in terms of calculation inputs and signs, especially with varying coordinate axes directions. Section 14.2.1 re-visits the concept of bending stress in order to discuss how to generalize the equations presented in Chapter 9 to any orientation of body with any arrangement of coordinate axes.
14.2.1 Generalized Bending Stress Equation
In Section 9.3, an equation for bending stress in the x direction based on bending around the cross-sectional axes y and z was derived. That equation is:
\[ \sigma_x=-\frac{M_z y}{I_z}+\frac{M_y z}{I_y} \]
The minus sign in front of the Mz term and the plus sign in front of the My term are part of the derived equation. When the correct signs for Mz, My, y, and z are inserted, the correct sign of the stress is obtained (positive for tensile and negative for compressive). In Chapter 9, no other cross-sectional axes were considered so that focus on the general concept of bending stress could be more easily maintained.
When the cross-sectional axes are not y and z, we apply the same general form of the above bending stress equation. However, for a different set of axes, not only do we need to change the bending moment and moment of inertia axes in the equation, we also need to reconsider the signs in front of each term. In any given bending load situation, the bending moments are the moments around the centroidal axes of the cross-section (V and H) and the resulting normal stress is in the longitudinal direction (L).
We can then re-frame the bending stress equation in a generalized form:
\[ {\sigma_{(bending)}= \pm\left|\frac{M_V\ d_H}{I_V}\right| \pm\left|\frac{M_H\ d_V}{I_H}\right|} \tag{14.1}\]
𝜎(bending) = Bending stress in the longitudinal direction [Pa, psi]
MV = Bending moment around the vertical axis of the cross-section [N⸱m, lb⸱in.]
MH = Bending moment around the horizontal axis of the cross-section [N⸱m, lb⸱in.]
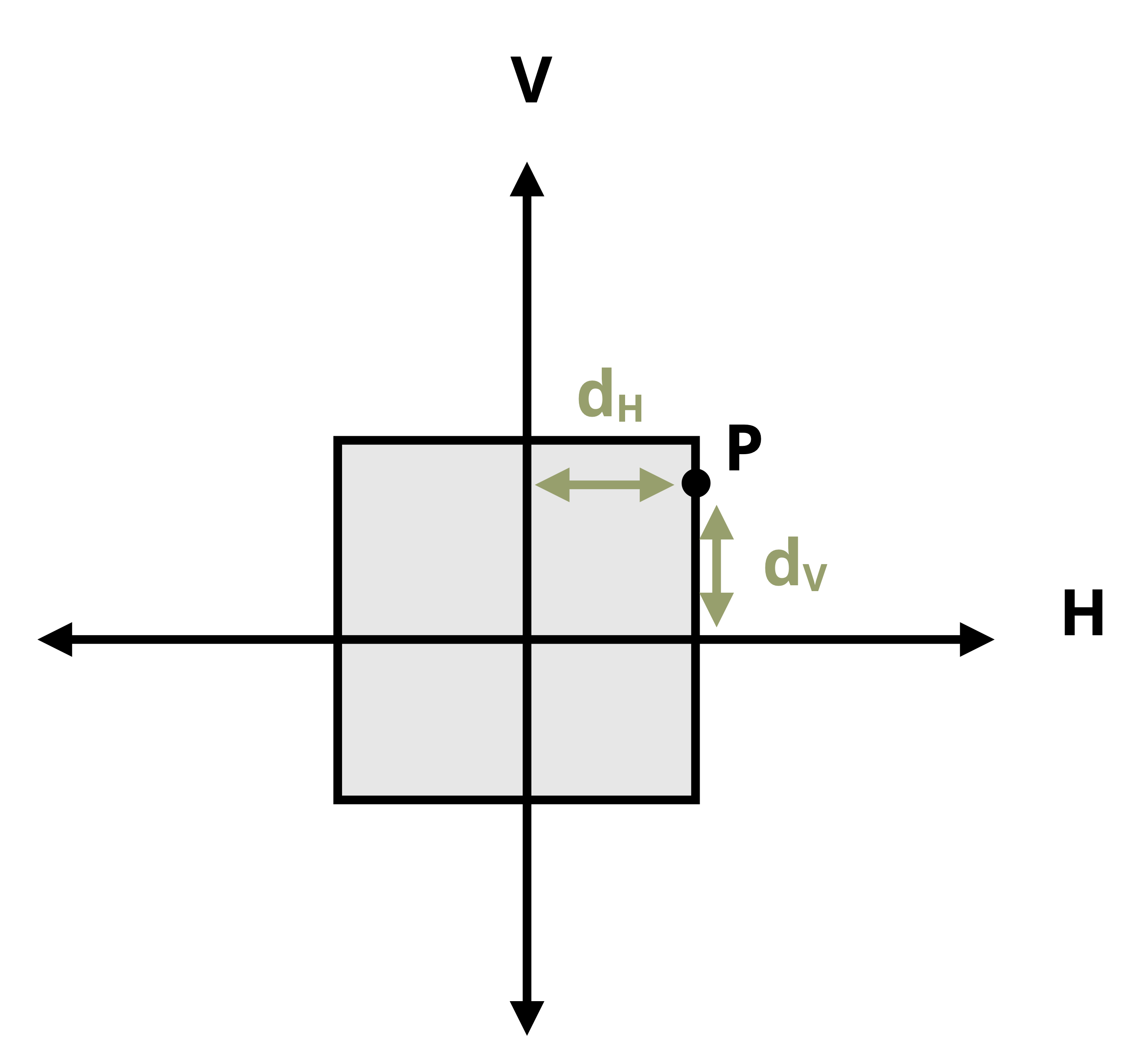
dH = Horizontal distance between the point of interest on the cross-section and the V axis [m, in.]
dV = Vertical distance between the point of interest on the cross-section and the H axis [m, in.]
IV = the moment of inertia about the vertical axis of the cross-section [m4, in.4]
IH = Area moment of inertia about the horizontal axis of the cross-section [m4, in.4]
Figure 14.3 illustrates the distances dH and dV for the case where the stress at the example point P on the cross-section is being calculated.
The absolute values are used for the bending stress terms with the +/- in front to indicate that we will calculate the magnitude of each bending stress term and then assess the signs of the terms independently. The assessment of the signs will be done by visualizing the bending direction, or by using visualization tools which will be described below. Recall that compressive stresses are considered negative and tensile stresses are positive.
In solving problems, it will be helpful to note that MH does not affect the normal stress of points directly on the H axis and MV does not affect the normal stress of points directly on the V axis. This is evident from the fact that dH =0 for a point on the V axis and dV =0 for a point on the H axis.
14.2.2 Assessing Bending Stress Signs For Generalized Bending Stress Equation
The sign on each of the two bending stress terms in Equation 14.1 needs to be determined by inspection of the bending direction. In Section 9.1, we saw that a bending moment around the horizontal axis causes the normal stress to vary along the vertical axis of the cross-section. In Section 9.3, we saw that a bending moment around the vertical axis causes normal stress to vary across the horizontal axis of the cross section. Which side is in tension versus compression in each case depends on the direction (clockwise versus counterclockwise) of the bending moment as well as the location of the point on the body.
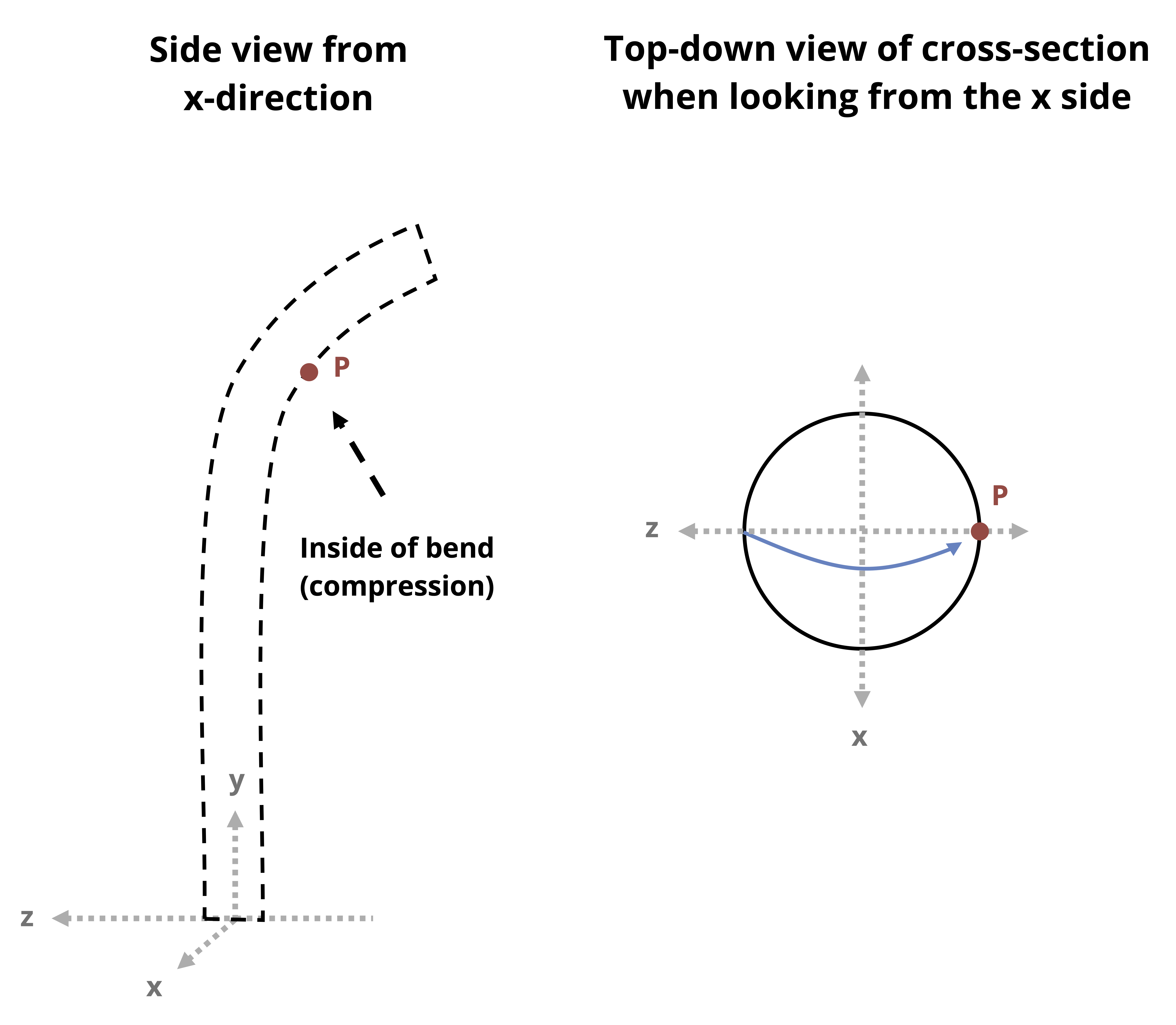
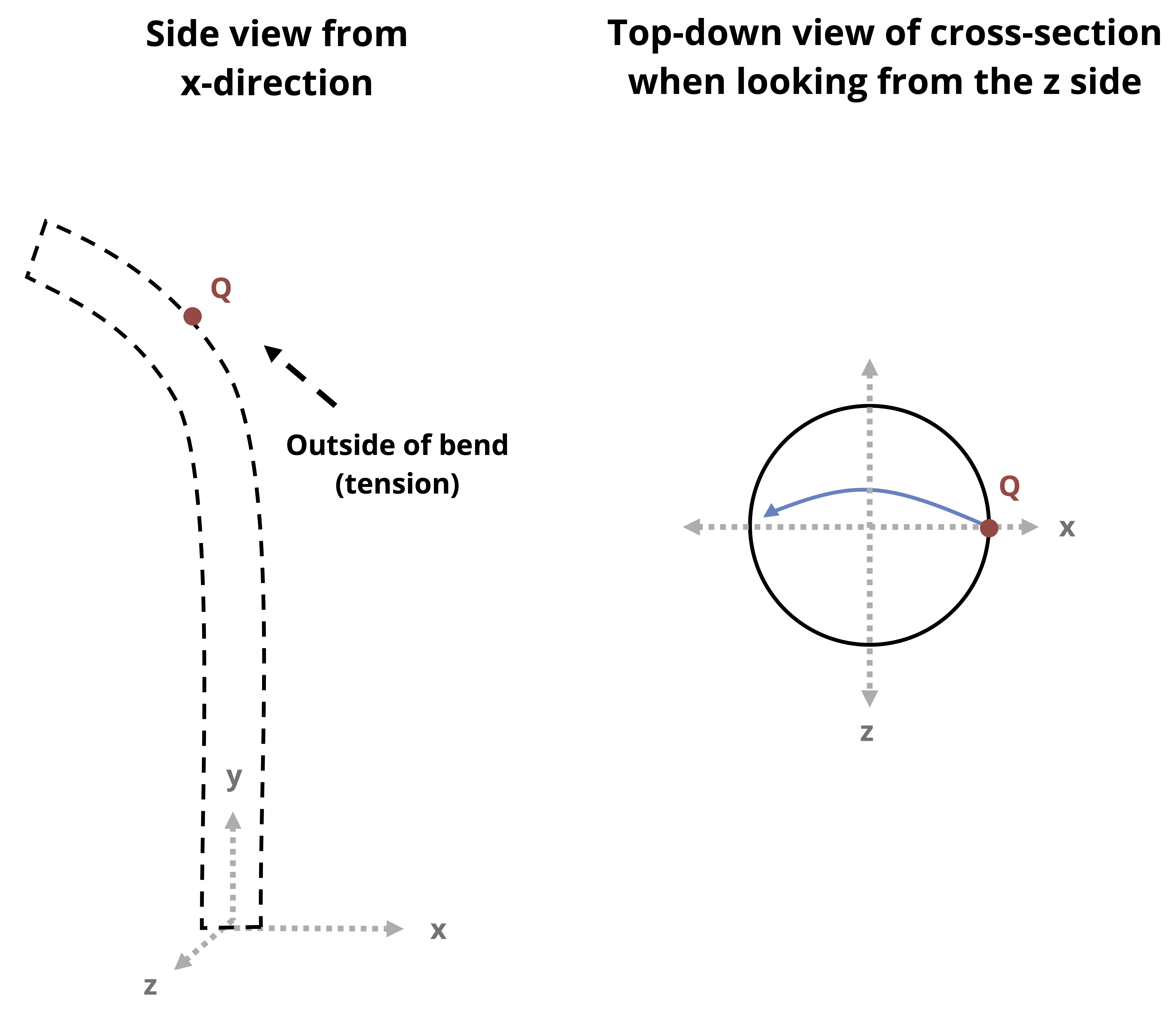
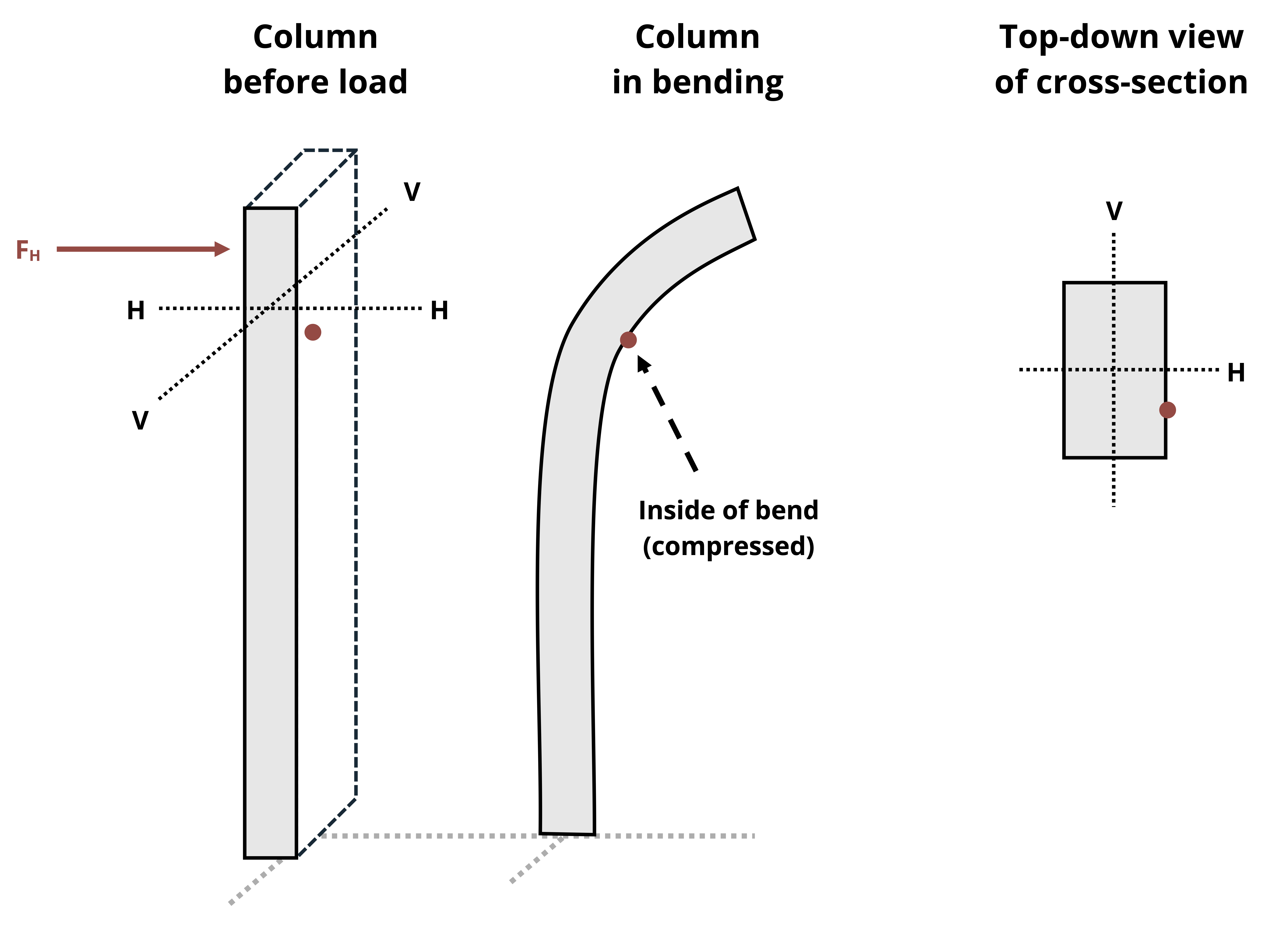
If we can visualize the expected bending direction due to loading, we can assess if a point will be on the “inside” of the bend (compression) or on the “outside” of the bend (tension). For example, in Figure 14.4, the rightwards horizontal force results in bending around the V axis of the cross-section. The direction of the bending is such that all points to the right of the V axis on the cross-section are on the inside of the bend (compression) and all points to the left of the V axis on the cross-section are on the outside of the bend (tension).
In Figure 14.5, the force in the V direction results in a bending moment around the H axis. The direction of the bending is such that all points above the H axis on the cross-section are on the inside of the bend (compression) and all points below the H axis on the cross-section are on the outside of the bend (tension).
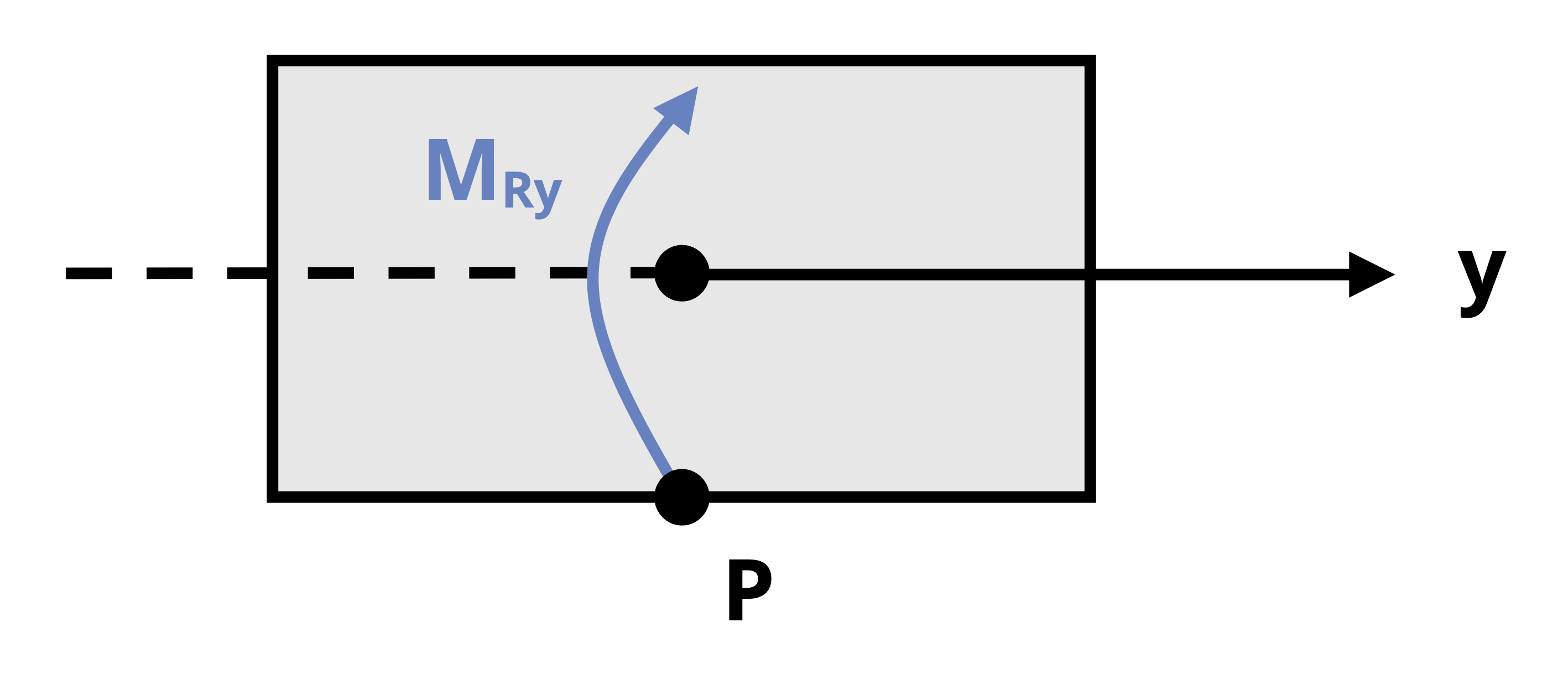
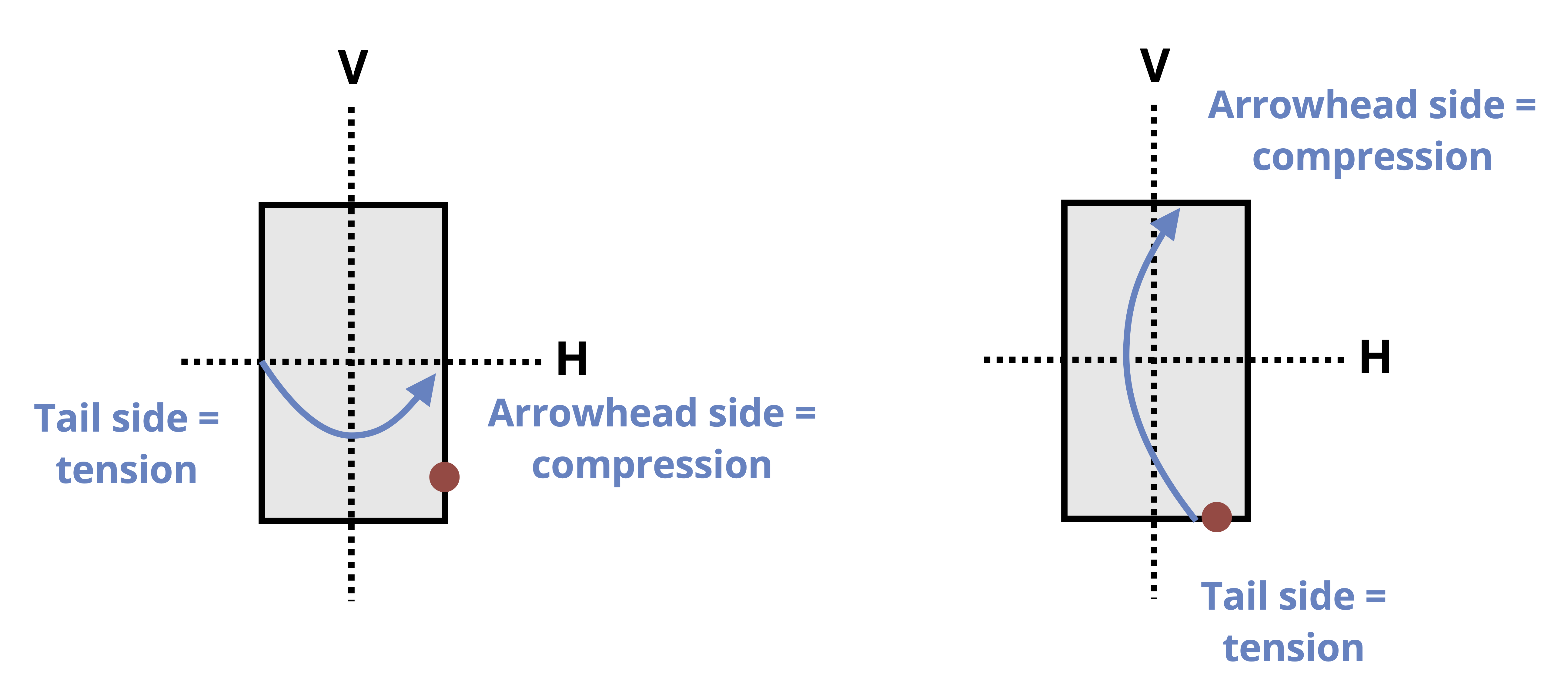
If visualization is difficult, one can use the following tool (refer to Figure 14.6):
- Draw the cross-section as viewed from the free end or cut end towards the origin. For example, in the case of the columns in Figure 14.4 and Figure 14.5, we would draw the top-down view of the cross-section.
- Draw the bending moment arrows around the V and H axes on the sketch of the cross-section. Exaggerate the arrows so they go all the way across.
- Make sure to draw the bending moment arrows such that they go over (or in front of) the bending axis (as opposed to under or behind)
- The side the arrowhead points to is the compressive side and the side the tail of the arrow is on is the tensile side.
The use of this tool will be demonstrated for the bending stress calculation in Example 14.1.
Example 14.1
The internal bending moments on a 32 mm diameter solid steel rod are found to be Mx = 376 kN mm (clockwise) and Mz = 204 kN mm (counterclockwise) as shown. Determine the bending stress at points P and Q.
1) Normally, we would draw the FBD of the cut section to find the internal bending moments. In this case, for simplicity, the internal moments are already given.
2) Write the general bending stress equation and eliminate unnecessary terms.
\[ \sigma_L= \pm\left|\frac{M_H\ d_V}{I_H}\right| \pm\left|\frac{M_V\ d_H}{I_V}\right| \]
Looking at the cross-section, we can see that the cross-sectional vertical axis is the z-axis and the cross-sectional horizontal axis is the x axis. The longitudinal axis is the y axis, so we have:
\[ \sigma_y= \pm\left|\frac{(M_z)\ (d_x)}{I_z}\right| \pm\left|\frac{(M_x)\ (d_z)}{I_x}\right| \]
Evaluating point P:
Because P is on the centroidal z-axis, dx = 0, and the general bending stress equation reduces to:
\[ \sigma_y= \pm\left|\frac{(M_x)\ (dz)}{I_x}\right| \]
3) Assess the sign:
With the clockwise bending moment around the x-axis, the beam can be visualized as bending “backwards” such that point P will be on the “inside” of the bend, or in compression. An approximation of the resulting shape is sketched below as it would appear from the side view (looking down the x-axis).
Alternatively, draw the cross-section with the exaggerated moment arrow clockwise around the x axis. Since the arrowhead would be pointed towards P, the point is in compression.
4) Calculate:
|Mx| = given = (376 kN mm)(1000 N/kN) = 376000 N mm
dz = radius = 16 mm
Ix =\(\frac{\pi}{64}d^4=\frac{\pi}{64}(32mm)^4=51.47\times10^3mm^4\)
\[ \begin{aligned} \sigma_{y_P}&=-\frac{376000{~N}\cdot{mm}\ (16mm)}{51.47 \times 10^{3}{~mm}^4}\\[10pt] &=-117{~N/mm^2}\\[10pt] &=-117\ MPa \end{aligned} \]
Evaluating Point Q:
Because point Q is on the centroidal x axis, dz = 0, so the general bending stress equation reduces to:
\[ \sigma_{y_Q}=\pm\left|\frac{(M_z)\ (dx)}{I_z}\right| \]
3) Assess the sign:
With the counterclockwise bending moment around the z-axis, the beam can be visualized as bending into somewhat of a backwards “C” shape as viewed from the front (down the z-axis). Point Q would be on the outside of the bend, or in tension.
Alternatively, draw the cross-section with the exaggerated moment arrow counterclockwise around the z-axis. Since Q is at the tail-side, the point is in tension.
4) Calculate:
|Mz| = given = (204 kN mm)(1000 N/kN) = 204000 N mm
dx = radius = 16 mm
For circular cross-section, Iz = Ix = 51.47 x 103 mm4
\[ \begin{aligned} \sigma_{y_Q}&=\frac{204000{~N}\cdot{mm}*(16{~mm})}{51.47 \times 10^{3}{~mm}^4}\\[10pt] &=63.4\ N/mm^2\\[10pt] &=63.4{~MPa} \end{aligned} \]
σyP = 116.9 MPa (compression)
σyQ = 63.4 MPa (tension)
14.2.3 Eccentric Loading
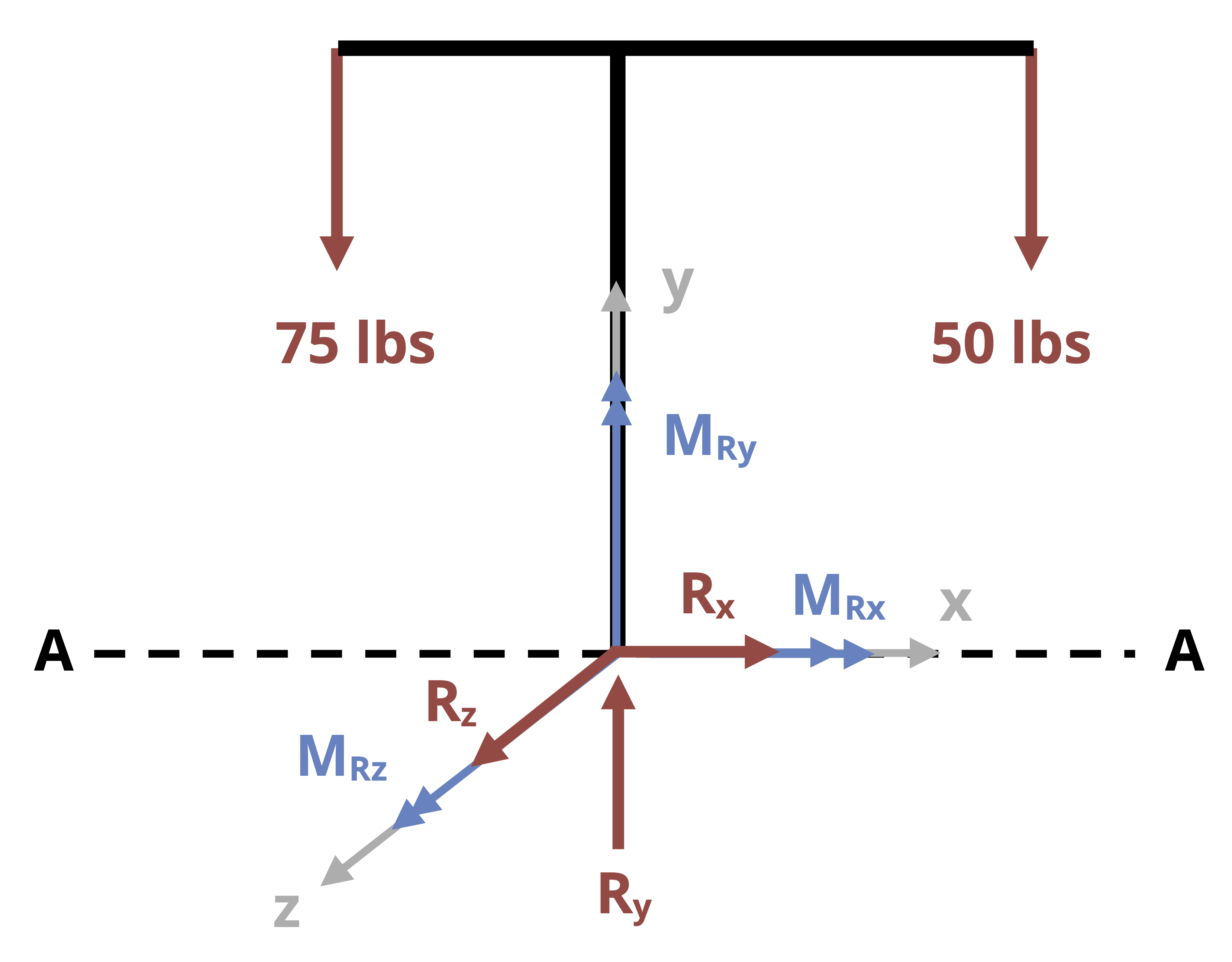
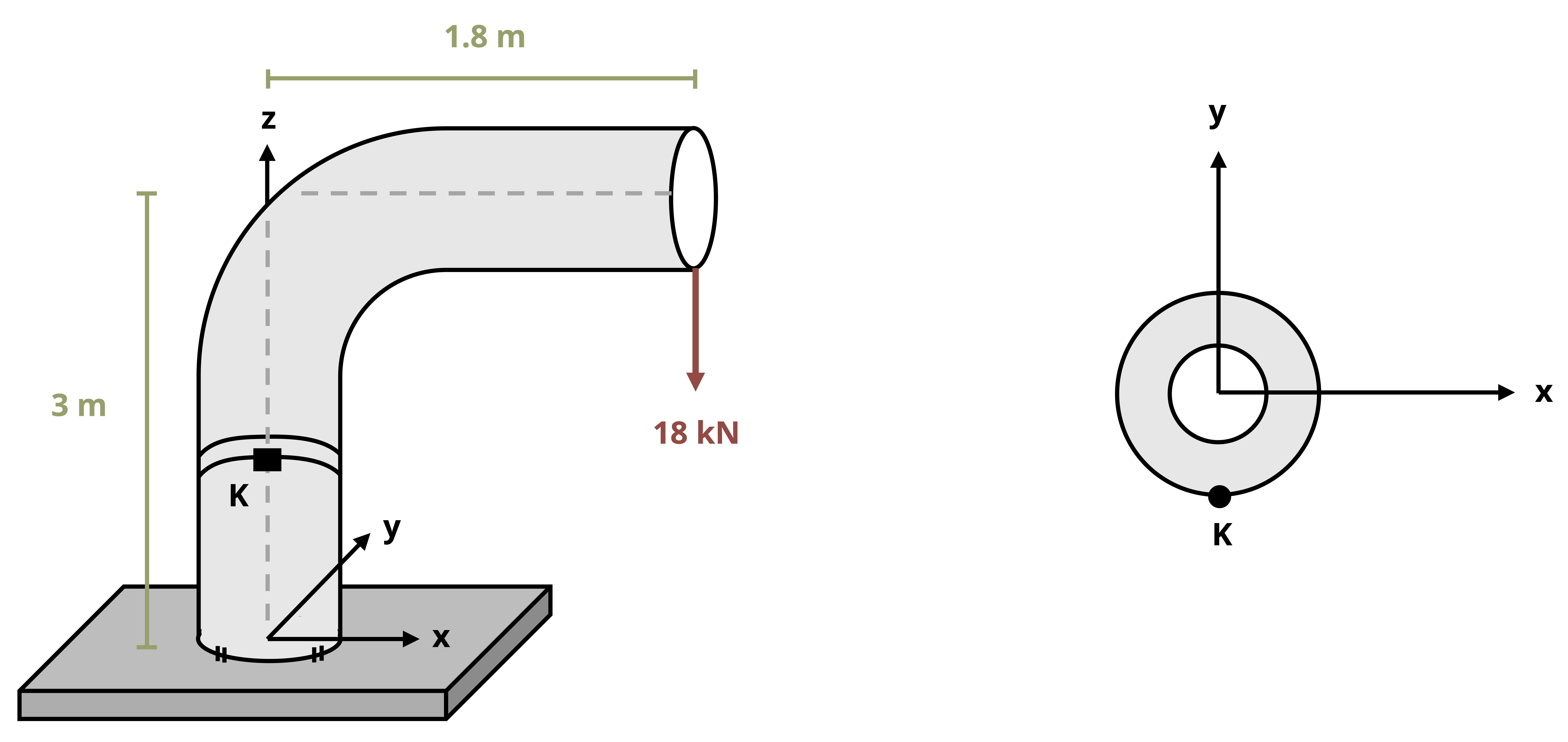
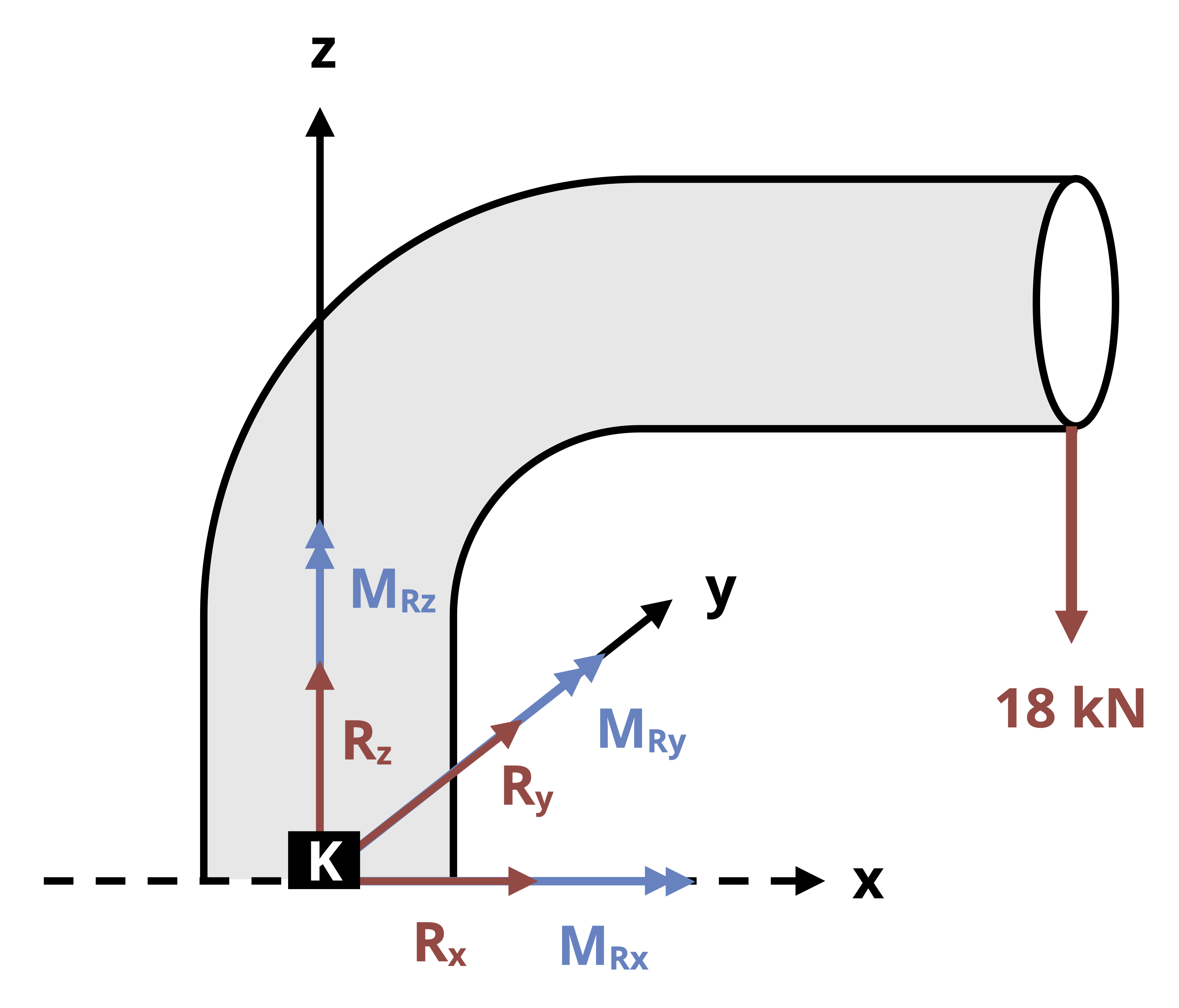
When the line of action of an axial load does not pass through the centroid of a cross section, it will result in both a normal reaction force and a bending moment. For example, consider the traffic light and corresponding free body diagram shown in Figure 14.7.
The vertical support pole is subjected to normal forces from the weights of the traffic lights (the weight of the horizontal poles, cameras, etc., are assumed to be negligible for this example). There are also bending moments around both cross-sectional axes (x and z) that result from the fact that the weights are not directly centered on the the support pole.
The total normal stress in the longitudinal direction, σL, at any given point on the pole would be given by:
\[ \sigma_L =\frac{\sum F_L}{A}+\sigma_{bending} \]
In terms of the general axes discussed in Section 14.1, and substituting in Equation 14.1 for the bending stress, we have:
\[ {\sigma_L= \pm\left|\frac{F_L}{A}\right| \pm\left|\frac{M_V\ d_H}{I_V}\right| \pm\left|\frac{M_H\ d_V}{I_H}\right|} \tag{14.2}\]
𝜎𝐿 = Bending stress in the longitudinal direction [Pa, psi]
FL = Internal normal force in the longitudinal direction [N, lb]
A = Cross-sectional area [m2, in.2]
MV = Bending moment around the vertical axis of the cross-section [N⸱m, lb⸱in.]
MH = Bending moment around the horizontal axis of the cross-section [N⸱m, lb⸱in.]
dH = Horizontal distance between the point of interest on the cross-section and the V axis [m, in.]
dV = Vertical distance between the point of interest on the cross-section and the H axis [m, in.]
IV = the moment of inertia about the vertical axis of the cross-section [m4, in.4]
IH = Area moment of inertia about the horizontal axis of the cross-section [m4, in.4]
The sign for the first term is positive if the FL is tensile (directed away from the cross-section) and negative if FLis compressive (pointed towards the cross-section).
Example 14.2 and Example 14.3 demonstrate the calculation of normal stress in eccentric loading problems.
Example 14.4 demonstrates a loading that includes pressure as part of the loading combination and drawing the resulting stress element.
Example 14.2
The structure is fixed to the ground and subjected to the 75 lb and 50 lb vertical forces shown. Determine the total normal stress at points P and Q on the cross-section located at A-A. Assume the 40 inch horizontal section at the top remains rigid.
1) Draw the FBD of the structure cut at A-A and write the equilibrium equations to find the internal reactions.
Below is the FBD for the section of the structure above the cut. Using the section above the cut allows us to avoid needing to calculate the reactions at the fixed support.
In this case, reaction forces Rx and Rz are 0 by inspection (we can see that there are no forces applied in those directions).
Similarly, reaction moments MRx and MRy are 0 by inspection: All the forces only act in the y direction, so MRy = 0. All the forces pass through the x-axis, so MRx = 0.
Calculating Ry and MRz:
\[\begin{aligned}\sum F_y=R_y-75{~lb}-50{~lb}=0 \quad\rightarrow\quad R_y=125{~lb}\end{aligned}\] \[\begin{aligned}\sum\ M_z &=\sum\pm(Fy*x)+\sum \pm\ (Fx*y)+M_{Rz}=0\\[10pt] &=(75{~lb}*15{~in.})-(50{~lb}*25{~in.})+M_{Rz}=0 \quad\rightarrow\quad M_ {Rz}=125{~lb}\cdot{in.}\end{aligned}\]
Remember when calculating reaction moments to calculate moments about the centroidal axes of the cross-section no matter where on the cross-section the point of interest is.
2) Write the generalized normal stress equation and eliminate unnecessary terms:
\[ \sigma_L= \pm\left|\frac{F_L}{A}\right| \pm\left|\frac{M_V\ d_H}{I_V}\right| \pm\left|\frac{M_H\ d_V}{I_H}\right| \]
In this case, the longitudinal axis is the y-axis. The vertical axis of the cross-section is the z-axis and the horizontal axis is the x-axis. With MRx = 0, we have:
\[ \sigma_y= \pm\left|\frac{R_y}{A}\right| \pm\left|\frac{M_{Rz}\ d_x}{I_z}\right| \]
3) Assess signs:
According to the equilibrium equations applied in step 2:
Ry points towards the cut section so it is compressive (negative). In addition, the force will affect all points on the cross-section in the same way, so the Ry/A term will be negative for both points P and Q.
MRz is counterclockwise for the section of the body above the cut at A-A. However, it tends to be easier to correctly visualize bending direction if we consider the bending moment for the section of the body attached to the fixed support. In this case, that is the section below the cut. Because the reactions on either side of the cut act in opposing directions ((equal/opposite reactions), the section attached to the fixed support is subjected to a clockwise bending moment.
The opposing reactions at the cut are shown below, as well as a sketch of the body bending clockwise around the z axis and a top down view of the cross-section with the moment arrow going clockwise around the z-axis.
Based on the above, we can see that point P will be in tension (outside of bend) from the bending stress and point Q will be compression (inside of bend).
4) Calculate the stress:
In addition to Ry and MRz, we need:
A = (6in.)(8in.) = 48 in.2
dx for point P = x-distance between P and the z-axis = 2 in
dx for point Q = x-distance between Q and the z-axis = 4 in
\(I_z = \frac{1}{12}bh^3=\frac{1}{12}(6{~in.})(8{~in.})^3 = 256{~in.^4}\)
Evaluating point P:
\[ \sigma_{yP}=-\left|\frac{125{~lb}}{48{~in.^2}}\right|+\left|\frac{(125{~lb}\cdot{in.})(2{~in.})}{256{~in.^4}}\right| \\ \sigma_{yP}=-1.63{~psi} \]
Evaluating point Q:
\[ \sigma_{yQ}=-\left|\frac{125{~lb}}{48{~in.^2}}\right|-\left|\frac{(125{~lb}\cdot{in.})(4{~in.})}{256{~in.^4}}\right| \\ \sigma_{yQ}=-4.56{~psi} \]
The negative answers indicates that the stress at both points is overall compressive.
Answers: σyP = -1.63 psi, σyQ = -4.56 psi
Example 14.3
The post is fixed to the ground and subjected to a 180 kN force pulling up at point P
Determine the normal stress at point A.
1) Draw the FBD of the structure cut at an arbitrary y-location and write the equilibrium equations to find the internal reactions.
For the given loading, the internal reactions will be the same for any y location, so we can make a cut anywhere to determine the bending moments and normal force reaction.
FBD above the cut:
The reaction forces Rz and Rx are 0 by inspection and the reaction moment MRy is also zero by inspection since the only applied force acts in the y direction.
\(\begin{aligned}\sum F_y=180 kN - R_y=0\quad\rightarrow\quad R_y=180 kN\end{aligned}\)
\(\begin{aligned}\sum M_x&=\sum\pm(Fy*z)+\sum\pm(Fz*y)+M_{Rx}\\[10pt]&=(180{~kN}*50{~mm})+M_{Rx}=0 \quad\rightarrow\quad M_{Rx}=-9000{~kN}\cdot{mm} \end{aligned}\)
\(\begin{aligned}\sum M_z&=\sum\pm(F_x*y)+\sum\pm(F_y*x)+M_{Rz}=0\\[10pt]&=(180kN*40mm)+M_{Rz}=0\quad\rightarrow\quad M_{Rz}=-7200\ kN\cdot mm\end{aligned}\)
2) Write the generalized normal stress equation:
Applying the generalized normal stress equation (with the pressure term omitted):
\[ \sigma_{L}= \pm\left|\frac{F_L}{A}\right| \pm\left|\frac{M_V d_H}{I_V}\right| \pm\left|\frac{M_H d_V}{I_H}\right| \]
In this case, the longitudinal axis of the post is the y-axis, the vertical axis of the cross-section is the z axis, and the horizontal axis of the cross-section is the x-axis. So we have:
\[ \begin{aligned} &\sigma_{yA}=\pm\left|\frac{R_y}{A}\right|\pm\left|\frac{M_z d_x}{I_z}\right|\pm\left|\frac{M_x d_z}{I_x}\right| \\ \end{aligned} \]
3) Assess the signs:
According to the equilibrium analysis, Ry points away from the cross-section, so that force results in tensile stress (positive).
The bending moments were both found to be clockwise for the section of the body above the cut. As was discussed in Example 14.2, to easier visualize the bending, we will use the direction of the bending moments on the section of the body where the fixed support is. In this case, the fixed support is attached to the section below the cut, for which the reaction moments will be opposite in direction to what we found in step 1. Thus, we visualize the column to bend counterclockwise around the x axis and the z axis.
The bending shapes that corresond to the two bending moments are shown below along with a sketch of the cross-section with the bending moment arrows represented. We can see that the bending moment around the x axis results in tension for point A but the bending moment around the z axis results in compression.
4) Calculate;
\[\sigma_{yA}=\left|\frac{R_y}{A}\right|-\left|\frac{M_z d_x}{I_z}\right|+\left|\frac{M_x d_z}{I_x}\right| \\ \sigma_{yA}=\left|\frac{180,000{~N}}{(0.2{~m})(0.15{~m})}\right|- \left|\frac{(7200{~N}\cdot{m})(0.085{~m})}{\frac{1}{12}(0.15{~m})(0.2 {~m})^3}\right|+\left| \frac{(9000{~N}\cdot{m})(0.075{~m})}{\frac{1}{12}(0.2{~m})(0.15{~m})^3}\right| \\[20pt]\sigma_{y A}=11.9 MPa \]
The stress works out to be positive and therefore tensile.
Answer: σyA =11.9 MPa
Example 14.4
For the pressurized pipe loaded as shown, determine the total normal stress at point K. Noting that there would be no shear stress at point K for this loading, represent the general stress state of point K on a stress element. The pipe has an outside diameter of 200 mm and a wall thickness of 10 mm. The load Pz = 18 kN and the internal pressure in the pipe is 1500 kPa.
1) Draw the FBD of the structure cut at point K and write the equilibrium equations to find the internal reactions.
FBD above the cut:
There are no forces in the x or y directions, so Rx= Ry =0.
The 18kN force is parallel to the z-axis and goes through the x-axis so MRz =MRx = 0.
MRy is not zero; however, point K is on the y-axis, so this point will not be affected by MRy (the x distance from the y-axis to point K on the cross-section is 0).
Thus, we do not need to calculate any moment reactions.
Calculating the reaction force in the y direction:
\(\sum F_z=R_z-18{~kN}=0 \quad\rightarrow\quad R_z=18{~kN}\)
2) Write the general normal stress equation and eliminate unnecessary terms. Note that the pressure loading will contribute to the longitudinal normal stress and will also result in normal stress in the cross-sectional directions (hoop stress):
\[ \sigma_L= \pm\left|\frac{F_L}{A}\right| \pm\left|\frac{M_V d_H}{I_V}\right| \pm\left|\frac{M_H d_V}{I_H}\right| + \frac{p r}{2 t} \]
\[ \sigma_{V}=\sigma_{H}=\sigma_{hoop}=\frac{pr}{t} \]
In this problem, the longitudinal direction is the z direction and the cross-sectional directions are x and y. Eliminating both bending stress terms, as discussed in step 1, leaves:
\[ \begin{aligned} \sigma_{zK} = \pm\left|\frac{R_z}{A}\right| + \frac{p r}{2 t} \\[10pt] \sigma_{x} =\sigma_y=\frac{p r}{t} \end{aligned} \]
3) Assess signs:
According to the equilibrium analysis, Rz points towards the cut section, so the first term in the stress equation will be negative. Internal pressure stress will always be positive.
4) Calculate:
\[ \begin{aligned} \sigma_{zK}&=-\left|\frac{R_z}{A}\right|+\frac{pr}{2t} \\[10pt] &=-\frac{18,000{~N}}{\pi\left(0.1^2-0.09^2\right){~m^2}}+\frac{(1,500,000{~Pa})(0.1{~m})}{2(0.01{~m})} \\[10pt] &=4.48{~MPa} \end{aligned} \]
\[ \sigma_x=\frac{pr}{t}=\frac{(1,500,000{~Pa})(0.1{~m})}{0.01{~m}}=15{~MPa} \]
5) Sketch the stress element, noting that point K is in the xz-plane.
14.3 General Shear Stress
Click to expand
Shear stress due to torsion was discussed in Chapter 6 while shear stress due to transverse loading was discussed in Chapter 10. In this section, the additional considerations that go into determining the total shear stress when both forms of loading are present will be discussed.
14.3.1 Shear Stress due to Torsion
As discussed in Section 6.0.1, shear stress due to torsion in a circular shaft can be calculated as (Equation 6.1):
\[ \tau_{(torsional)}=\pm\left|\frac{T \rho}{J}\right| \]
where:
\(T=Torque=\sum M_L\) [N m, lb in.]
𝜌 = radial distance from center to the point of interest on the cross-section [m, in.]
J = polar moment of inertia for circular cross-section [m4, in.4]
Once again, as was done for the normal stress equations, the +/- and absolute value is used to signify that we will calculate the magnitude of the stress and assess the sign inpendently.
For general problems, one may need to sum moments to calculate T, so it is important to remember that torque is the moment about the longitudinal axis of a body, or that component of the moment that causes the body to twist. Since this form of shear stress will be combined with transverse shear stress to get the total, understanding the sign of the shear stress will be important.
As discussed in Section 12.1, the sign of shear stress is based on the orientation of the shear stress arrows on the stress element that represents the stress state of the point of interest.To determine in which direction to draw a shear stress arrow on a stress element for a particular point, one must cut the body at one edge of the stress element and visualize the direction in which the shear load would act across the cut.
For example, in Figure 14.8 below, the stress element is shown to be in the L-H plane. When the cylinder is cut at the top of the stress element, we examine the bottom section of the cylinder and note that the reaction torque at the cut surface should be opposite in direction to that which is applied at the bottom surface. This results in a counterclockwise (from the top view perspective) reaction torque at the cut, which means that the top section tends to want to twist (and exert a force) from left to right across the top edge of the stress element.
If the longitudinal axis is positive upwards, the top face of the element is a positive L face. In addition, if the horizontal axis is positive to the right, the rightwards shear force arrow acts in the positive H direction. A positive H force on the positive L face constitutes a positive shear stress.
Similarly, when the cut is made at the bottom edge of the element, we can examine the top section of the cylinder, for which equilibrium dictates that there is a clockwise (again, based on top view) reaction moment at the cut edge. This means that the bottom section tends to want twist from right to left across the bottom element edge. The right to left arrow on the bottom face of the element represents a negative H force on a negative L face. The double negative indicates a positive shear stress, confirming the result obtained above from studying the bottom section of the cylinder.
If the H axis were to be oriented to be positive to the left instead, then this same shear stress would be negative. The same can be said if the H axis is positive to the right but the L axis is positive downwards.
14.3.2 Shear Stress due to Transverse Shear Force
In Chapter 10, the equation \(\tau=\frac{V Q}{I t}\) (Equation 10.2) was evaluated to find the shear stress due to a transverse shear force V that arises from a non-constant bending moment. In that chapter, only one direction of shear force was considered for each problem and the sign of the shear stress was not evaluated.
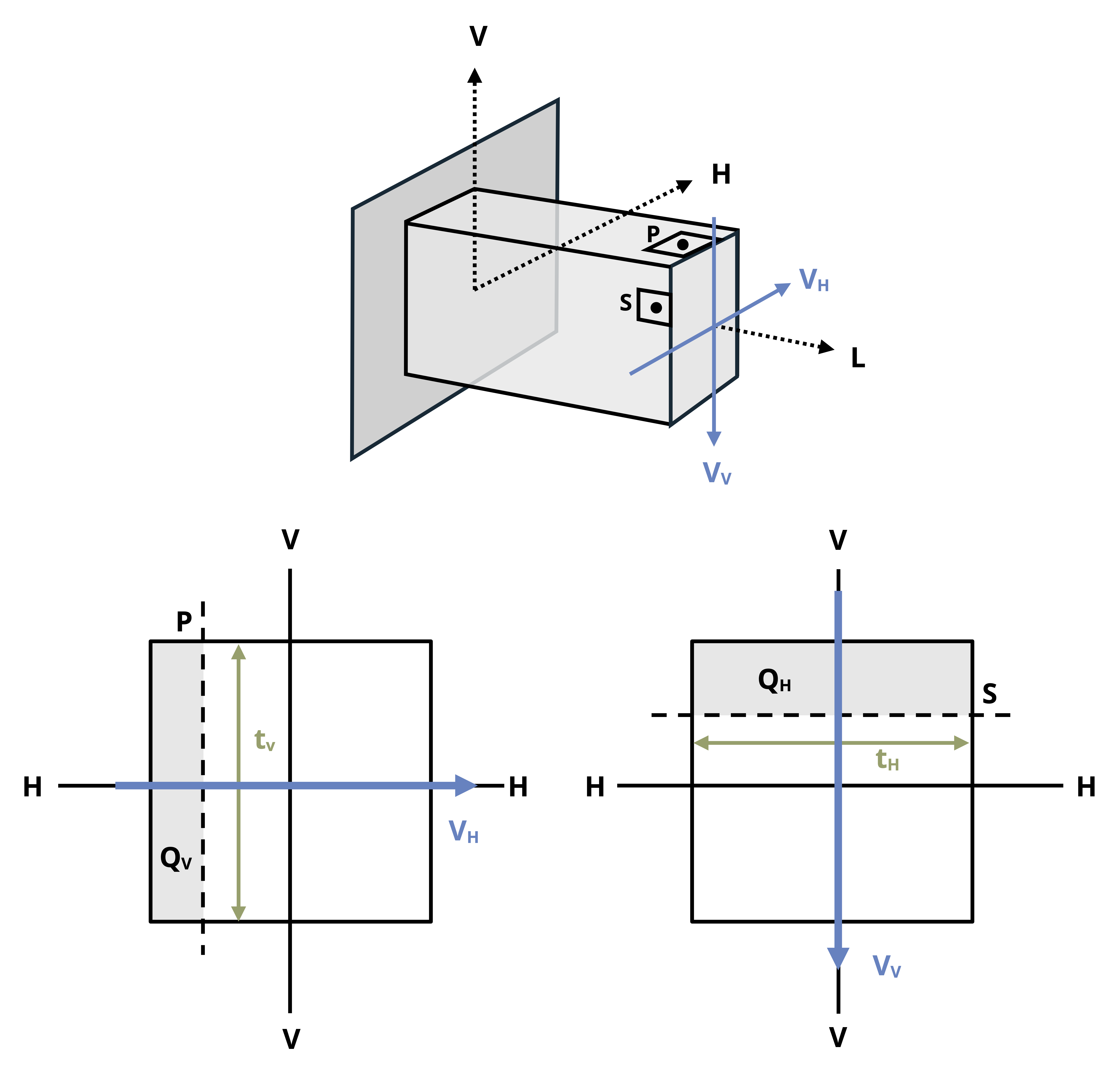
For general loading, we may have two directions of transverse shear force corresponding to the two cross-sectional axes directions, as shown on the illustration of the bar in Figure 14.9. In this case, we will need to apply the transverse shear stress equation for both directions and also understand the signs so that we can combine them with each other and with the torsional shear stress. The direction of the shear force will affect the direction of the cut made across the cross-section to find Q and t and the axis the moment of inertia is based on.
When applying the transverse shear stress equations for specific directions of shear force, it is helpful to keep the following in mind:
- The cut on the cross-section one makes to determine the first moment of area Q will be perpendicular to the direction of shear force direction (illustrated on the cross-sections in Figure 14.9).
- The area moment of inertia (I) will be based on the axis perpendicular to the shear force direction.
- The thickness (t), refers to the thickness of the solid part of the cross section that one cuts through to calculate Q (illustrated on the cross-sections in Figure 14.9).
Using the same reference axes as were used in the general normal stress equation (H for horizontal cross-sectional axis and V for vertical cross-sectional axis), the transverse shear stress equation can be written as follows:
\[ {\tau_{(transverse)}= \pm\left|\frac{V_H Q_V}{I_V t_V}\right| \pm\left|\frac{V_V Q_H}{I_H t_H}\right|} \tag{14.3}\]
𝜏(transverse) = Transverse shear stress at point of interest [Pa, psi]
VH = Internal horizontal shear force [N, lb]
VV = Internal vertical shear force [N, lb]
QV = First moment of area about the vertical axis passing through the point of interest [m3, in.3]
QH = First moment of area about the horizontal axis passing through the point of interest [m3, in.3]
IV = Area moment of inertia about the vertical centroidal axis of the cross-section [m4, in.4]
IH = Area moment of inertia about the horizontal centroidal axis of the cross-section [m4, in.4]
tV = Vertical thickness of the cross-section cu through [m, in.]
tH = Horizontal thickness of the cross-section cut through [m, in.]
When assessing the contributions to shear stress present for any given point, a simplifying observation that can be made is:
1) If a point is on the top or bottom edge of a non-circular cross-section, or is the top or bottom point of a circular cross-section, it will experience no transverse shear stress from a vertical shear force.
2) If a point is on the left or right edge of a non-circular cross-section, or is the left most or right most point of a circular cross-section, it will feel no transverse shear stress from a horizontal shear force.
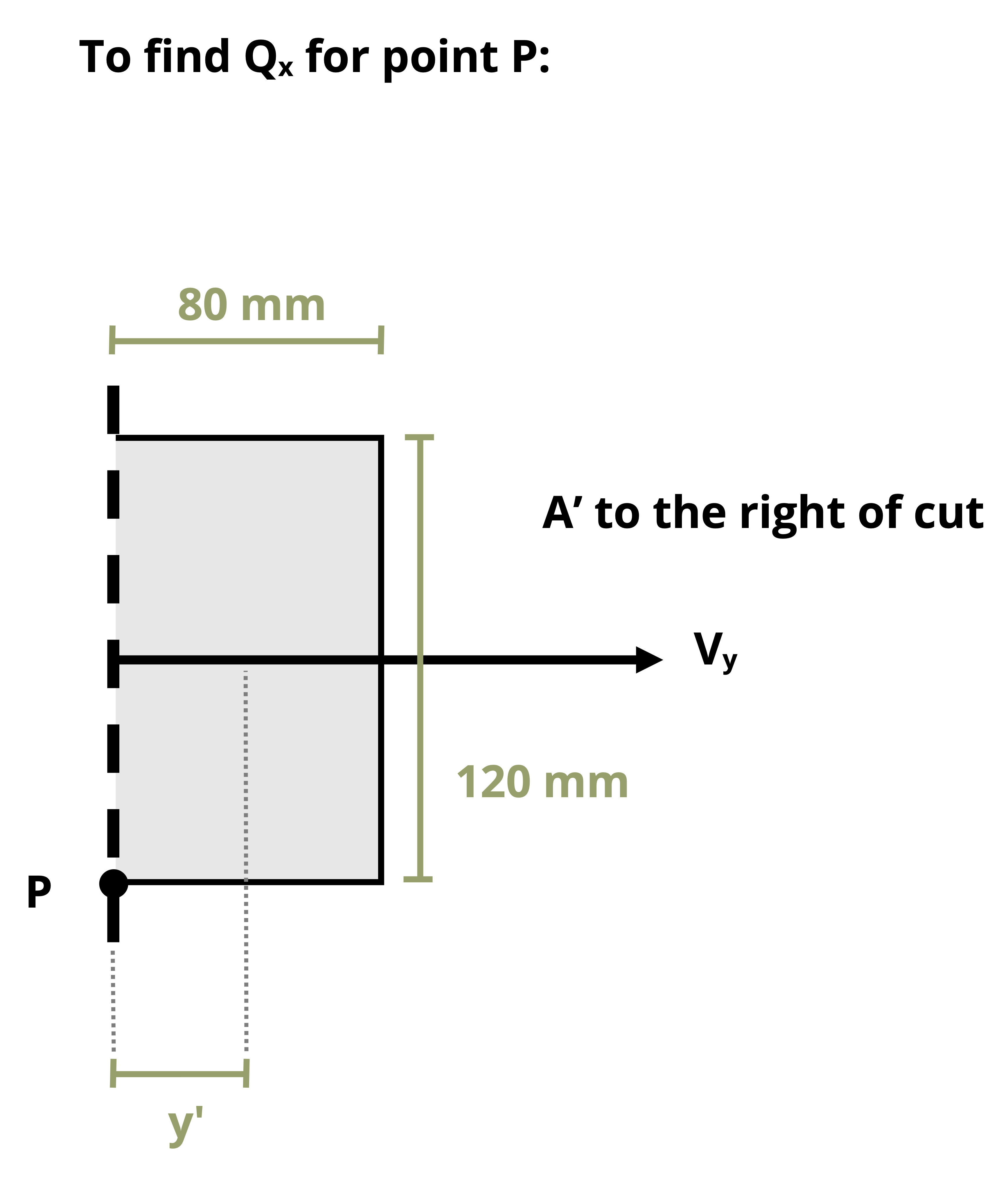
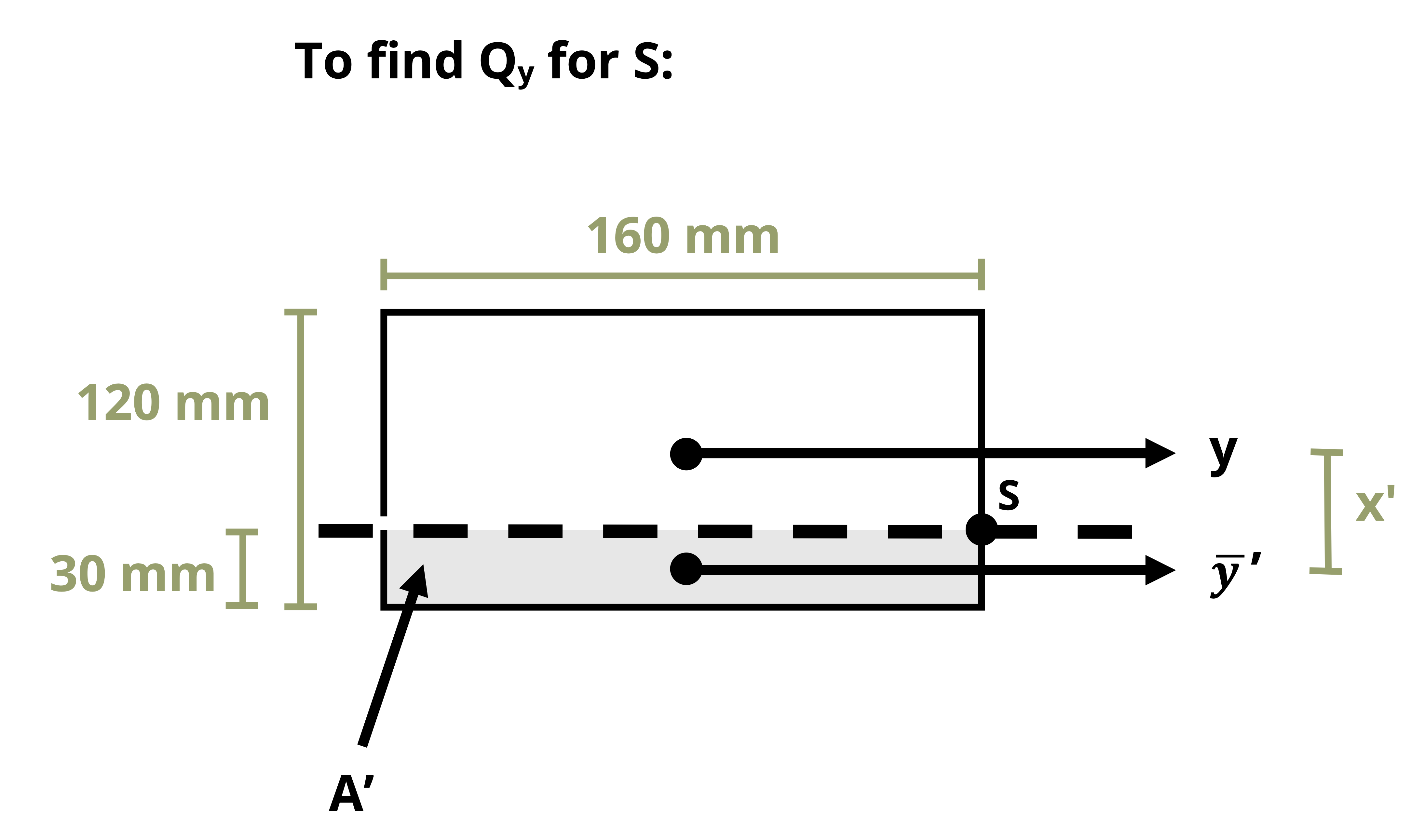
For example, in Figure 14.9, point P will experience no shear stress from VV and point S will feel no shear stress from VH. Figure 14.10 further illustrates the statements above.
The reason for this is that, in the case of a vertical shear force, bending is around the H axis so the top and bottom edges of the cross-section are free edges. Similarly, in the case of a horizontal shear force, bending is around the V axis so the left and right edges of the cross-section are free surfaces. For a circular cross-sections, the idea is similar, but only applies to the points at the top/bottom and left/right positions along the centroidal axes on the perimeter. Another way to think about is that Q = 0 for the top and bottom edges in the case of a vertical shear force and for the left and right edges for a horizontal shear force.
The signs on the shear stress are determined similarly to the manner described in Section 14.3.1 for torsion. The direction of the internal shear force is determined by cutting hte body at the point of interest, drawing the FBD of the cut section, and applying equilibrium. The resulting shear stress is considered to act in that same direction on the cut surface of the element.
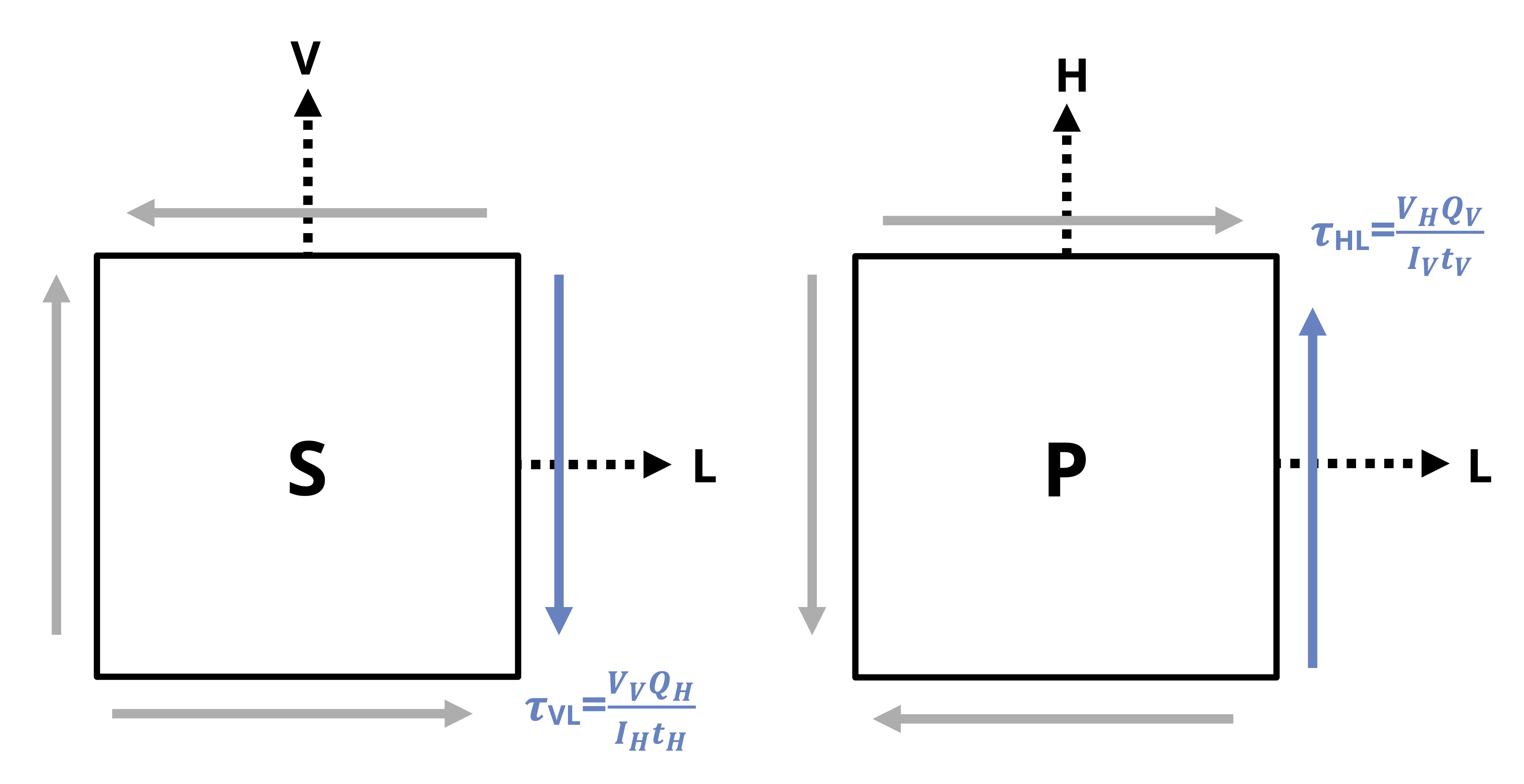
For example, in Figure 14.9, point S is on the V-L plane. ?fig-14.11 shows the element drawn from the side view, looking down the H axis. The shear force VV acts downwards on the right side of the stress element. With the axes oriented such that the longitudinal axis is positive to the right, the right side of the stress element is the +L face. If the V axis of the element is positive upwards, than VV is acting in the negative V direction on the +L face, indicating a negative shear stress.
Similarly, point P is on the H-L plane. In ?fig-14.11, the stress element is drawn from the top view (viewing down the V axis). The shear force VH acts upwards on the right side of the stress element. If the right side is the +L face, and the H axis is positive upwards, then VH acts in the +H direction on the +L face, indicating a positive shear stress.
14.3.3 Combined Shear Stress
Now we can consider the case of bodies simultaneously subjected to both torsion and transverse shear stresses. Given a general loading situation, one may need to calculate the torque and also identify which of the forces constitute transverse shear forces. It will be helpful to remember:
The transverse shear forces are the internal forces in the directions of the cross-sectional axes.
Torque is the internal moment about the longitudinal axis
- Also recall that in this text, torsion is only considered for circular cross-sections.
The total shear stress acts in the plane of the point of interest. It can be calculated as:
\[ {\tau= \pm\left|\frac{T \rho}{J}\right| \pm\left|\frac{V_H Q_V}{I_V t_V}\right| \pm\left|\frac{V_V Q_H}{I_H t_H}\right|} \tag{14.4}\]
𝜏 = Shear stress at point of interest [Pa, psi]
T = Internal torque [N·m, lb·in.]
𝜌 = Radial distance from centroid to point of interest [m, in.]
J = Polar moment of inertia [m4, in.4]
VH = Internal horizontal shear force [N, lb]
VV = Internal vertical shear force [N, lb]
QV = First moment of area about the vertical axis passing through the point of interest [m3, in.3]
QH = First moment of area about the horizontal axis passing through the point of interest [m3, in.3]
IV = Area moment of inertia about the vertical centroidal axis of cross-section [m4, in.4]
IH = Area moment of inertia about the horizontal centroidal axis of cross-section [m4, in.4]
tV = Vertical thickness of the cross-section at cut made for QV [m, in.]
tH = Horizontal thickness of the cross-section at cut made for QH [m, in.]
Example 14.5 demonstrates the calculation of total shear stress when torsion and transverse shear are both acting.
Example 14.6 demonstrates the calculation of transverse shear stress with multiple directions of shear force.
Example 14.5
A solid steel bar with an outside diameter of 6.70 in. is fixed to the wall. A 900 lb force acts vertically and a 1500 lb force acts in the positive x direction as shown. Determine the maximum shear stress at points J and K on the outside of the pipe.
1.) Cut the body at the cross-section where K and J are located and apply equilibrium to the FBD of the cut section to find the internal reactions.
We will examine the section to the right of the cut to avoid needing to find the reactions at the wall.
The cross-sectional axes are the x and z axes, so these are the bending moment and transverse shear directions. The y axis is perpendicular to the cross-section, so it is the longitudinal axis.
Before proceeding with equilibrium calculations, we note that we are only asked to find shear stress. Therefore, we do not need to know the bending moments MRx and MRz and we do not need to know the normal force Ry.
The shear forces are the forces in the cross-sectional directions (Rx and Rz). We find them by applying the force equilibrium equations:
\(\begin{aligned}& \sum F_x=R_x+1500 lb=0\quad\rightarrow\quad R_x=V_x=-1500 lb \\& \sum F_z=R_z+900{~lb}=0 \quad\rightarrow\quad R_z=V_z=-900{~lb}\end{aligned}\)
The torque is the moment about the longitudinal axis (MRy). We find it by applying the moment equilibrium equation for the y axis. Note that on the FBD, the direction of MRY is assumed to act counterclockwise around the y axis when viewing from the positive end to the negative (right to left).
\(\sum M_y=M_{Ry}+(900{~lb})(18{~in.})=0 \quad\rightarrow\quad M_{Ry}=T=-16,200{~lb\ in} \\\)The negative result means that the torque acting at the cut side of the FBD we drew is clockwise around the y axis when viewing from the positive side towards the negative (right to left).
2) Write the general shear stress equation and eliminate unnecessary terms:
\[ \tau= \pm\left|\frac{T \rho}{J}\right| \pm\left|\frac{V_H Q_V}{I_V t_V}\right| \pm\left|\frac{V_V Q_H}{I_H t_H}\right| \]
The horizontal axis of the cross-section is the x-axis and the vertical axis is the z axis.
Point K is on the yz plane. Since point K is on the x axis, it will not experience shear stress from Vx.
Point J is on the xy plane. Since point J is on z axis, it will not experience shear stress from Vz.
\[ \tau_{Kyz}= \pm\left|\frac{T \rho}{J}\right| \pm\left|\frac{V_z Q_x}{I_x t_x}\right| \]
\[\tau_{Jxy}= \pm\left|\frac{T \rho}{J}\right| \pm\left|\frac{V_x Q_z}{I_z t_z}\right|\]
3) Assess the signs.
For the torsional stress term:
If we consider the stress element for each point to be just inside of the cut section we used to find the internal reactions, as shown in the figure below, we can see that the left side of each element will be the side that the calculated internal shear loads act on.
Based on the direction of MRY found in step 1, illustrated in the diagram below, we can see that it acts in an upwards direction across the left face of both stress elements. This is indicated with the blue arrow and T label on the stress elements drawn below. For point K, this results in a negative contribution to the shear stress (positive z force on negative y face) but for point J, it will be a positive shear stress (negative x force on negative y face).
For the shear forces:
Rz was found to act in the negative z direction so it will act downwards on the left face of the stress element for point K. The resulting shear stress will be positive.
Rx was found to act in the negative x direction so it will act upwards on the left face of the stress element for point J. This shear stress will also be positive.
Now we have:
\[\tau_{Kyz}= -\frac{T \rho}{J}+\frac{V_z Q_x}{I_x t_x} \]
\[\tau_{Jxy}= \frac{T \rho}{J} +\frac{V_x Q_z}{I_z t_z} \]
4) Calculate:
For a circular cross-section:
\(Q_x=Q_z=\frac{1}{12}d^3=\frac{1}{12}(6.70\ in)^3=25.06\ in^3\)
\(I_x=I_z=\frac{\pi}{64}d^4=\frac{\pi}{64}(6.7\ in)^4=98.92\)
\(J=\frac{\pi}{32}d^4=\frac{\pi}{32}(6.7\ in)^4=197.83\ in^4\)
So for point K:
\[\begin{aligned}\tau_{Kyz}&= -\frac{T \rho}{J}+\frac{V_z Q_x}{I_x t_x}\\[10pt] &=\frac{(-16200\ lb\ in)(\frac{6.70\ in}{2})}{197.83\ in^4}+\frac{(900\ lb)(25.06\ in^3)}{(98.92\ in^4)(6.70\ in)}\\[10pt] &=-274.3\ psi+34.04\ psi\\[10pt] &=-240.3\ psi \end{aligned} \]
For point J, the torsional shear stress will be the same magnitude, so we have:
\[ \begin{aligned}\tau_{Jxy}&=274.3\ psi+\frac{(1500\ lb)(25.06\ in^3)}{(98.92\ in^4)(6.7\ in)}\\ &=331.0\ psi \end{aligned} \]
Answers: τKyz = -240.27 psi, τJxy = 331.02 psi
Example 14.6
Two forces are applied to a rectangular post fixed to the ground support as shown. Determine the shear stress at points P and S.
1) Draw the FBD of the structure cut at at the vertical location where P and S are located and apply equilibrium to find the internal reactions.
FBD of the section above the cut:
The cross-sectional axes are the x and y axes, so these are the bending moment and transverse shear directions. The z axis is perpendicular to the cross-section, so it is the longitudinal axis.
While we can see by inspection Rz = 0, it is also not necessary to find since it only contributes to normal stress.
Similarly, the bending moments MRx and MRy are not necessary to find for this problem since they would also only contribute to the normal stress. However, this problem is re-visited in Example 14.7 and those moments are found in that example.
Since both of the applied forces pass through the centroidal z-axis, MRz = T = 0.
Find the internal shear forces using force equilibrium equations:
\(\sum F_x=R_x-94\ kN=0\quad\rightarrow\quad R_x=V_x=94 kN\)
\(\sum F_y=R_y+78\ kN=0\quad\rightarrow\quad R_y=V_y=-78\ kN\)
2) Write the general shear stress equation and eliminate unnecessary terms. Ignoring the torsion term since T = 0 (and we have a non-circular cross-section), the general shear stress equation can be written:
\[ \tau= \pm\left|\frac{V_H Q_V}{I_V t_V}\right| \pm\left|\frac{V_V Q_H}{I_H t_H}\right| \]
Where the horizontal axis of the cross-section is the y–axis and the vertical axis of the cross section is the x-axis.
As discussed in Section 14.3.2, since point P is on the bottom edge of the cross-section (from the top view), it will not experience shear stress from Vx. Similarly, point S is on the right edge of the cross-section (also from the top view), so it will not experience shear stress from Vy.
This leaves us with:
\[\tau_{Pyz}=\pm \left|\frac{V_y\ Qx}{I_x\ t_x}\right| \]
\[ \tau_{Sxz}=\pm \left|\frac{V_x\ Qy}{I_y\ t_y}\right| \]
3) Assess the signs.
Since we used the section above the cut to calculate internal reactions, we consider the stress elements to be at the bottom of the top section, just inside the cut surface, as shown in the FBD in step 1. The shear forces then act on the bottom face of the stress elements.
Point P is on the xy plane and point S is on the xz plane. Both stress elements are shown below with axes positive in the indicated directions.
Vy was found to act in the negative y direction, so it gets drawn directed to the left at the bottom of the P stress element. This results in a positive shear stress for point P.
\[\tau_{Pyz}=\frac{V_y\ Q_x}{I_x\ t_x} \]
Vx was found to act in the positive x direction. so it gets drawn directed to the left at the bottom of the S stress element. This results in a negative shear stress for point S.
\[\tau_{Sxz}=-\frac{V_x\ Q_y}{I_y\ t_y} \]
4) Calculate.
\(V_H = V_y = 78{~kN}\)
\(V_V = V_x = 94{~kN}\)
\(I_H=I_y=\frac{1}{12}(160{~mm})(120{~mm})^3=23.04 \times 10^6{~mm}^4=23.04 \times 10^{-6}{~m}^4\)
\(I_V=I_x=\frac{1}{12}(160{~mm})^3(120{~mm})=40.96 \times10^6{~mm}^4=40.96 \times 10^{-6}{~m}^4\)
For point P we need Qx and tx. Cutting vertically through point P on the cross-section:
\[ \begin{aligned}&Q_x=A'y'=\frac{1}{2}(160{~mm})(120{~mm})*\left(\frac{1}{2}\right)(80{~mm})=384000{~mm}^3=384 \times 10^{-6}{~m}^3\\[10pt] &t_x=120\ mm = .12\ m \end{aligned} \]
For point S we need Qy and ty. Cutting horizontally through point S on the cross-section:
\(\begin{aligned}&Q_y=A'x'=(160{~mm})(30{~mm})*(60{~mm}-15{~mm})=216000{~mm}^3=216 \times 10^{-6}{~m}^3\\[10pt]&t_y=160\ mm=.16\ m\end{aligned}\)
So
\[ \tau_{Pyz}=\frac{V_y Q_x}{I_x t_x}=\frac{(78000{~N})(384 \times 10^{-6}{~m}^3)}{(40.96 \times 10^{-6}{~m}^4)(0.12{~m})}=6.09{~MPa} \]
\[ \tau_{Sxz}=-\frac{V_x Q_y}{I_y t_y}=-\frac{(94000{~N})(216 \times 10^{-6}{~m}^3)}{(23.04 \times 10^{-6}{~m}^4)(0.16{~m})}=-5.51{~MPa} \]
Answers:
τPyz = 6.09 MPa
τSxz = -5.51 MPa
14.4 General Combined Stress
Click to expand
Once the total normal stress and total shear stress at a specified point is calculated, the general stress state can be represented on a stress element and used to determine principal stresses, principal planes, and max/min shear stresses.
In Example 14.7, the problem from Example 14.6 is extended to find the principal stresses and max/min shear stresses.
Example 14.7
Re-examine Example 14.6 to find the principal stresses and max/min shear stresses for point P on the post:
In Example 14.6 the total shear stress for point P was found to be positive 6.09 MPa.
To find the principal stresses, we must:
finish finding the general stress state by also finding the total normal stress and
use the principal stress equations or Mohr’s Circle.
To complete the first task:
1) Again, use the FBD of the section of the post above the cut made at the vertical location of P and S to find the relevant internal reactions.
We know from Example 14.6 that Rx = 94 kN and Ry = - 78 kN.
By inspection, we can see that Rz = 0.
Point P is on the x axis, so we know that it will not experience any bending stress from MRx .
As noted in the previous example, MRy = 0 by inspection, but it would not contribute to the normal stress in any case since that would be a torsional moment.
Thus, the only bending moment reaction we need to calculate is MRy . Using the moment equilibrium equation for the y-axis:
\(\begin{aligned}\sum M_y&=(-94{~kN})(150{~mm})+M_{Ry}=0\\ &=-14,100{~kN\ mm}+M_{Ry}=0\quad\rightarrow\quad M_{Ry}=14,100{~kN\ mm}\end{aligned}\)
2) Write the generalized normal stress equation (noting that there is no pressure loading):
\[ \sigma_{L}= \pm\left|\frac{F_L}{A}\right| \pm\left|\frac{M_V d_H}{I_V}\right| \pm\left|\frac{M_H d_V}{I_H}\right|\\ \]
From the top down view of the cross-section shown above, we see that the vertical axis of the cross–section is the x-axis and the horizontal axis is the y-axis. The z axis is the axis perpendicular to the cut surface, so it is the longitudinal axis. So the generalized normal stress equation can be rewritten with the given axes as:
\[ \sigma_z=\pm\left|\frac{R_z}{A}\right|\pm\left|\frac{(M_{Rx})(d_y)}{I_x}\right|\pm\left|\frac{(M_{Ry})(d_x)}{I_y}\right| \]
With Rz = 0 and point P located on the x axis (see discussion in step 1), we can reduce the equation to:
\[ \sigma_{Pz}=\pm \left |\frac{(M_{Ry})\ (x)}{I_y}\right| \]
3) Assess the sign.
To assess the sign, we note that we determined the reaction moment at the cut surface of the upper section of the post to be positive, or counterclockwise. That means the reaction moment at the cut surface for the lower section of post (beneath the cut at P and S) will be clockwise. As mentioned in Example 14.2 and Example 14.3, we want to use the bending moment on the section attached to the fixed support (the lower section in this case) to visualize the bending.
With a clockwise bending moment around the y-axis, looking from the side view down the y-axis, the post would look like it curves around to the right, placing point P on the outside of the bend (tension).
Alternatively, drawing the cross-section from the top view, with the clockwise moment arrow drawn around the y-axis, we can see that point P is on the tail side of the cross-section, confirming tension at this point.
So \(\sigma_{Pz}=+\frac{(M_Ry)\ (d_x)}{I_y}\)
4) Calculate.
Recalling \(I_y = 23.04 \times 10^{-6}{~m^4}\) from Example 14.6, the normal stress at P is:
\[ \begin{aligned} \sigma_{Pz}&=\frac{(M_{Ry})( d_x)}{I_y}\\[10pt] &=\frac{14,100{~N}\cdot{m}\ (0.06{~m})}{23.04 \times 10^{-6}{~m^4}}\\[10pt] &=36.77{~MPa} \end{aligned} \]
Now we can now find the principal stresses and max/min shear stress:
Start by representing the general stress state on a stress element.
We can use the simplified version of the principal stress and the max/min shear equation (Equation 12.5); however, these equations were generally written for stresses in the xy plane:
\[ \begin{aligned} & \sigma_{1,2}=\frac{\sigma_x+\sigma_y}{2} \pm \sqrt{\left(\frac{\sigma_x-\sigma_y}{2}\right)^2+\tau_{x y}{ }^2} \\[10pt] & \tau_{\max , \min }= \pm \sqrt{\left(\frac{\sigma_x-\sigma_y}{2}\right)^2+\tau_{x y}{ }^2} \end{aligned} \]
In this problem, point P is on the yz-plane. Based on the discussion at the end of Section 12.2.2., we can replace the x subscripts with y and the y subscripts with z, and calculate:
\[ \begin{aligned} \sigma_{1,2}&=\frac{\sigma_y+\sigma_z}{2}\pm\sqrt{\left(\frac{\sigma_y-\sigma_z}{2}\right)^2+\tau_{yz}^2}\\[10pt] &=\frac{0+36.77{~MPa}}{2} \pm \sqrt{\left(\frac{0-36.77{~MPa}}{2}\right)^2+(6.094{~MPa})^2}\\[10pt] &=37.75{~MPa}, -.984{~MPa} \\ \end{aligned} \]
\[ \begin{aligned} \tau &=\pm\sqrt{\left(\frac{\sigma_y-\sigma_z}{2}\right)^2+\tau_{yz}^2}\\[10pt] &=\pm\sqrt{\left(\frac{0-36.77 MPa}{2}\right)^2+(6.094 MPa)^2}\\[10pt] &=\pm 19.37 MPa \end{aligned} \]
Answers:
σ1 = 37.75 MPa
σ2 = -.984 MPa
τmin = -19.37 MPa
τmax = 19.37 MPa
14.5 Summary
Click to expand
References
Click to expand
Figures
All figures in this chapter were created by Kindred Grey in 2025 and released under a CC BY license.