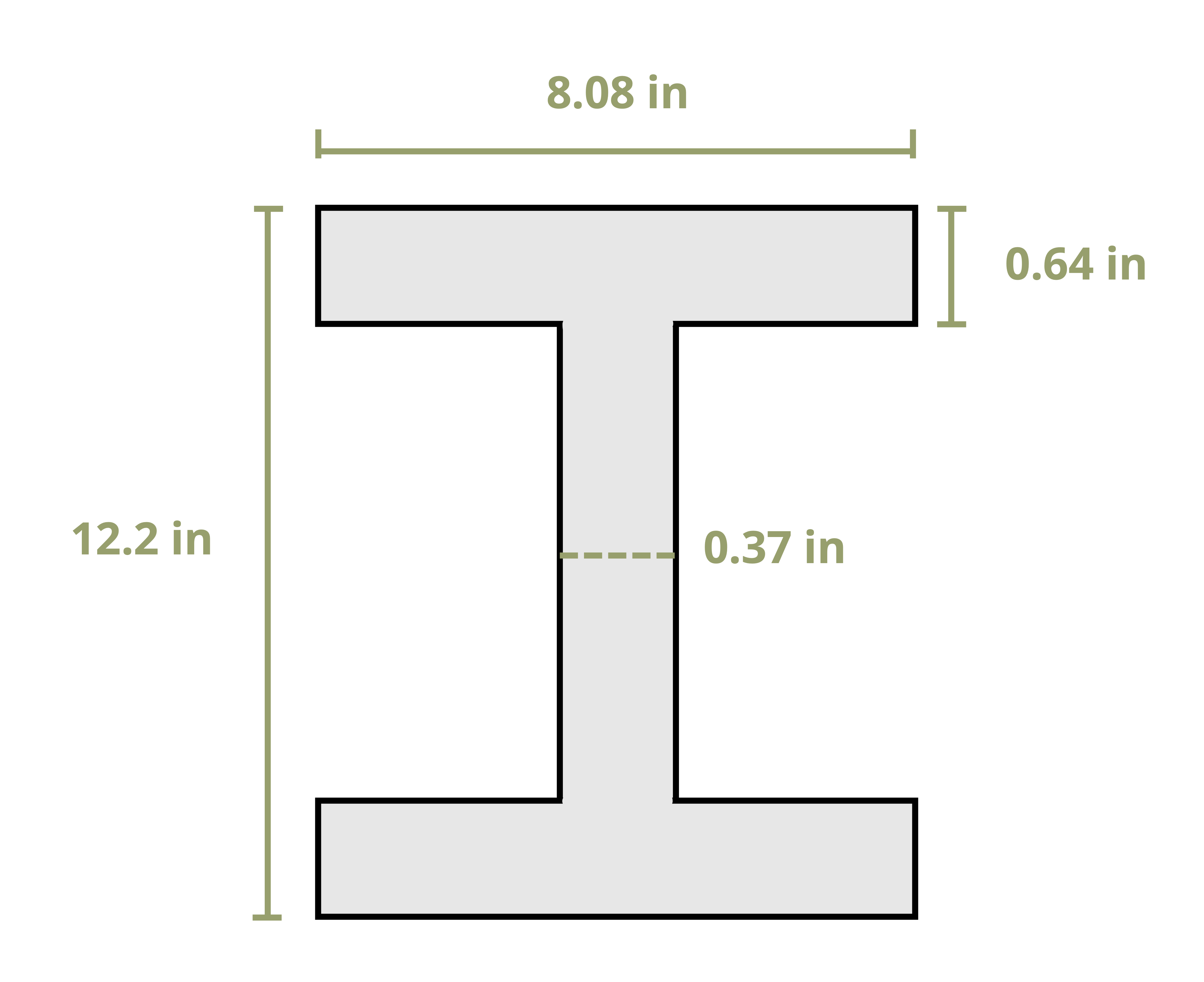
15  Columns

NoteLearning Objectives
  • Describe column buckling behavior
  • Construct the equation known as Euler’s formula for columns
  • Differentiate end conditions to calculate an appropriate effective length

Until now our focus has been primarily on meeting strength and deflection criteria. While these aspects are crucial, it’s equally important to ensure a structure’s stability. This chapter therefore delves into the stability analysis of long and slender members subjected to compressive loading, commonly referred to as columns. Some examples are shown in Figure 15.1. When the compressive load reaches a critical point, columns may undergo sudden sideways deflection, a phenomenon known as buckling. After buckling, a column is unable to support any further load. This chapter focuses on long, slender, homogeneous, axial compression members, otherwise known as columns.

Section 15.1 derives the buckling formula for columns that are supported by pin connections at both ends. Section 15.2 extends this to consider other common end conditions.

Three types of column-supported structures arranged side by side. Image A, on the left, features decorative cast-iron columns with riveted flanges and flared bases and capitals, supporting steel girders in an industrial or transit setting. Image B, in the center, shows a modern construction interior with rectangular reinforced-concrete columns arranged in a grid pattern, supporting concrete slabs and surrounded by exposed brick walls. Image C, on the right, depicts a reconstructed wooden post-and-beam structure with round timber columns and an open gabled roof frame, likely representing an ancient or traditional building system displayed in a museum setting.
Figure 15.1: Examples of columns

15.1 Euler’s Formula for Buckling

Click to expand

Even in ideal conditions, buckling often occurs for long, slender members at loads significantly lower than the material’s crushing or compression limit. When a long, slender object is subjected to axial loading, it may buckle once the load reaches a critical threshold known as the critical load, Pcr. At this point the object experiences significant lateral deflection perpendicular to the load direction, so columns should be designed such that the applied load does not exceed the critical load.

Buckling of a ruler (long, slender member) is depicted in Figure 15.2. The ruler in the left and center photos is subjected to axial load, P, that is less than critical load, Pcr. This is known as stable equilibrium. In the photo on the right the axial load P exceeded the critical load Pcr, causing a significant lateral deflection. This is known as unstable equilibrium.

Figure demonstrating buckling behavior using a thin flexible ruler under axial compressive force, shown in three images side by side. In the first image (left), equal and opposite red arrows labeled P are applied vertically to the ends of a straight ruler, with the front face of the ruler visible. In the second image (middle), the same compressive forces labeled P are applied, but the side face of the ruler is shown instead. In the third image (right), the compressive force is increased so that P is greater than P sub cr, and the ruler, still viewed from the side, buckles into a curved shape, illustrating classical elastic buckling under a critical load.
Figure 15.2: Buckling of a ruler

15.1.1 Stability

We can consider stability by using a simplified model of a pinned-pinned column. This column consists of two ridged bars connected with a pin and a spring with a stiffness k, as the free body diagram (FBD) shows in Figure 15.3 (A). When the load, P, is small, the system remains vertical and the spring is unstretched. If point C is displaced to the right a small amount, Δ, the spring will produce a force F = kΔ, as shown in Figure 15.3 (B). This force is used to resist the horizontal forces, Px = Ptanθ, as shown in Figure 15.3 (C).

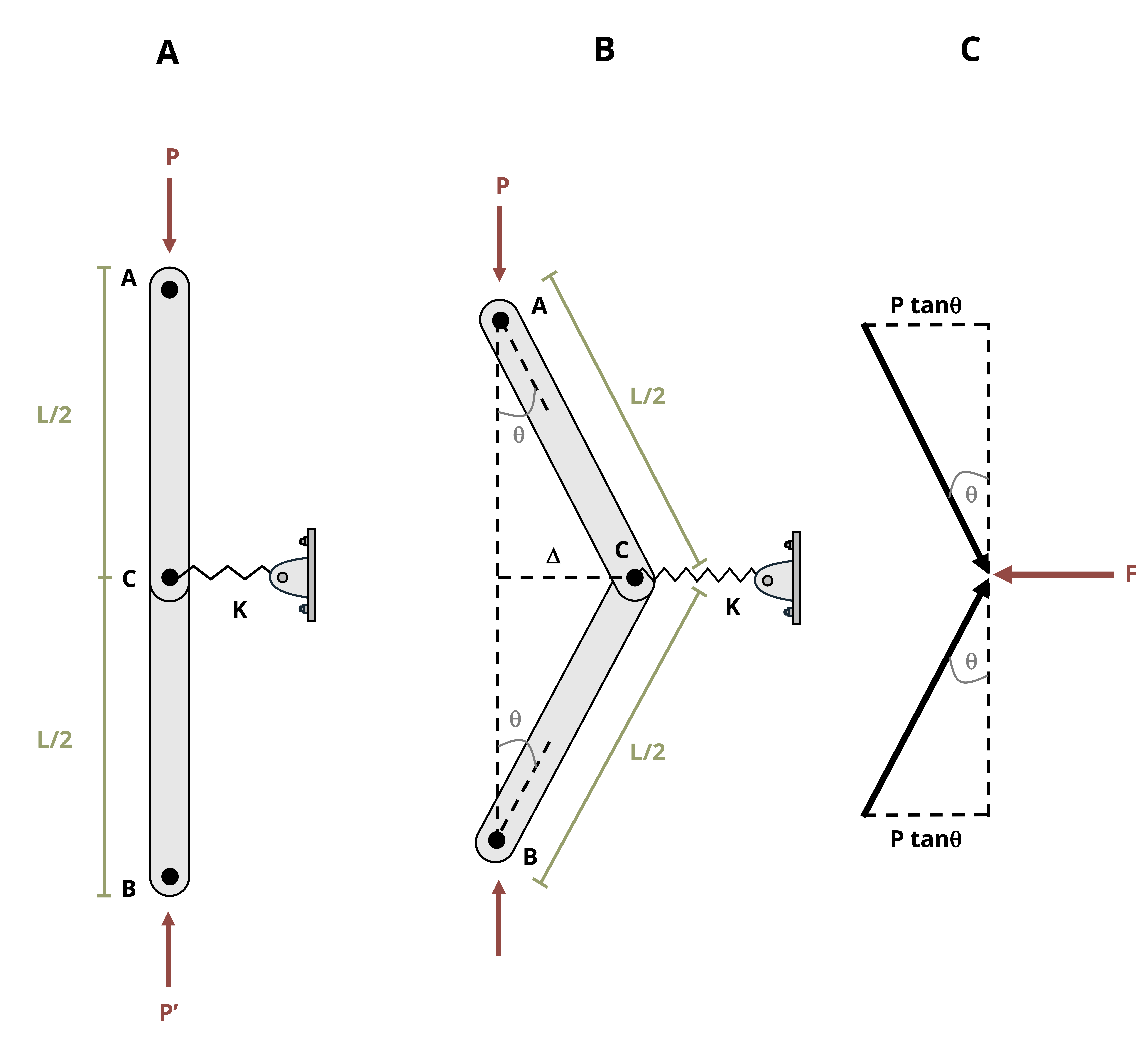
Figures labeled A, B, and C are shown side by side, illustrating the buckling and internal force behavior of a pinned–pinned column with a lateral spring. In diagram A (left), vertical compressive forces labeled P and P prime are applied at the ends of a vertical column AB: P acts downward at point A, and P prime acts upward at point B. The column is connected at its midpoint, point C, to a pin where a spring of stiffness K extends horizontally from the pin to a fixed pin support. The column is initially straight, with a total length labeled L, divided equally into two segments of L over 2. In diagram B (middle), the column has buckled under the compressive load, forming two inclined segments that meet at the midpoint C. A lateral deflection labeled delta is shown with a dashed line extending horizontally left from point C, and the angles between the vertical reference line and the members AC and BC are both labeled theta. The spring remains attached at point C, maintaining stiffness K and connected to the same pin support. In diagram C (right), a free-body diagram of the buckled state is shown. The internal force in member AC acts diagonally downward toward the southeast, while the force in member BC acts diagonally upward toward the northeast. A horizontal red arrow labeled F represents the spring force acting leftward. Horizontal dashed lines extend rightward from the diagonal forces and are labeled P times tan theta. A vertical dashed line passes through the intersection of these dashed lines, forming two symmetric triangles. The angle between each diagonal force and the vertical dashed line is labeled theta, the upper triangle includes theta as the downward angle, and the lower triangle includes theta as the upward angle.
Figure 15.3: Free body diagram of a simplified column

Since θ is small

\[ \sin \theta \sim \theta \text { and } \tan \theta \sim \theta \]

Consequently

\[ \Delta=\theta \frac{L}{2} \text { and } 2 P_x=2 P \theta \]

Using the spring restoring force equation F = kΔ, then substituting in for Δ, results in

\[ F=k \theta \frac{L}{2} \]

If the spring restoring force is greater than the axial force, then equilibrium is stable.

\[ \begin{aligned} & F>P \\ & k \theta \frac{L}{2}>2 P \theta \end{aligned} \]

The θ cancels out, and we can solve for P.

\[ P<\frac{k L}{4} \]

Similarly, we can solve for the expression for unstable equilibrium F < P.

\[ P>\frac{k L}{4} \]

The point at which F = P is crucial because it is the line between stable and unstable equilibrium. This is known as the critical load Pcr.

\[ P_{c r}=\frac{k L}{4} \]

Thus if the load P exceeds Pcr, the system will be unstable. If P is less than Pcr, the system will be stable. Pcr is used in the next section to determine the buckling load of columns.

15.1.2 Euler’s Formula

As mentioned in earlier sections, members can fail due to material yielding or fracturing. However, instability represents another critical failure mechanism that requires consideration. Here Euler’s formula can be used to calculate the theoretical buckling load. To do this we’ll start with the simplest of columns, pinned-pinned end connections. This means that the column cannot translate but can rotate as shown in Figure 15.4.

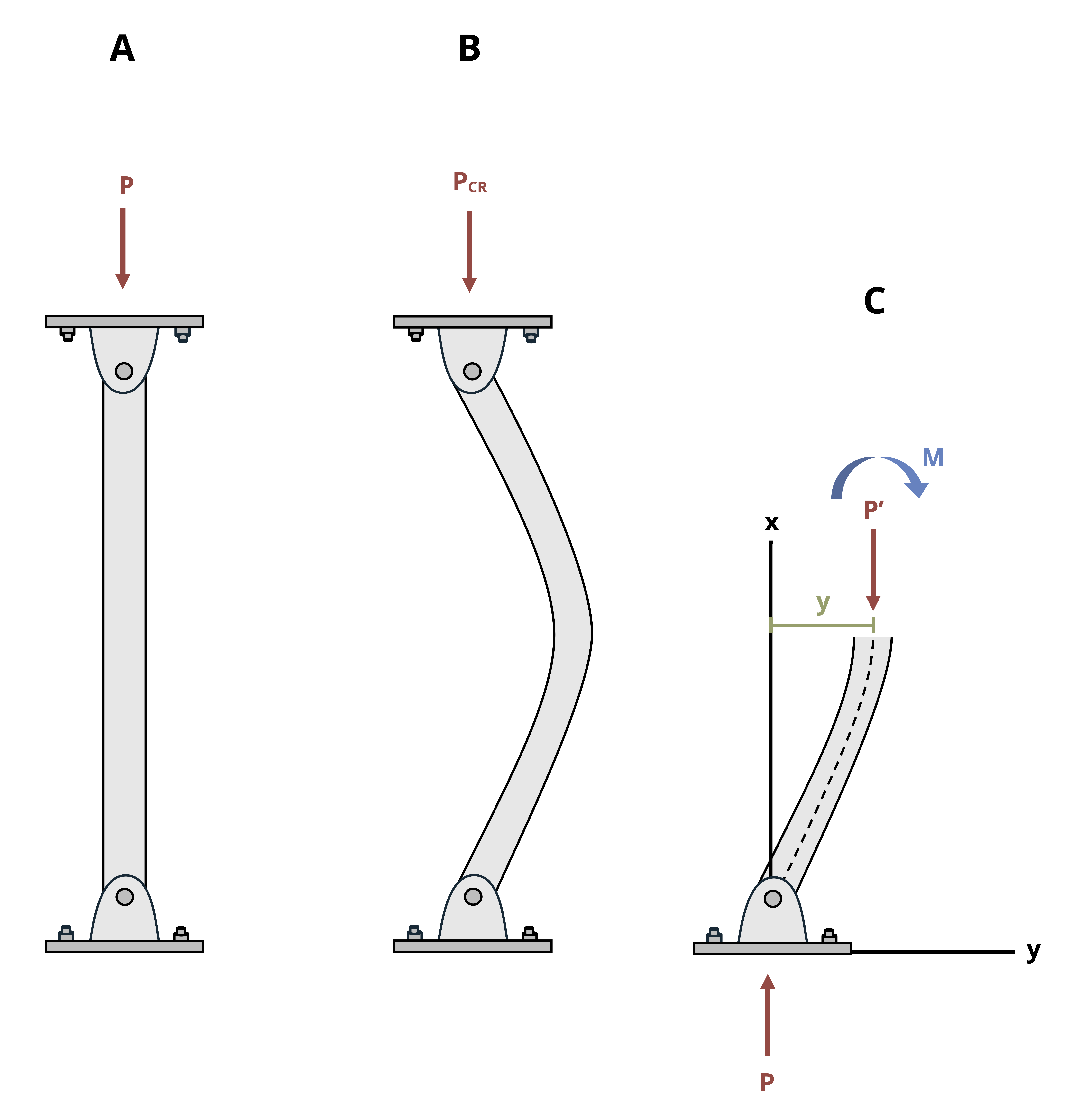
Figures labeled A, B, and C are shown side by side, illustrating the buckling of a pinned-pinned axially loaded rectangular column. In diagram A (left), a straight vertical column is compressed by a downward force labeled P applied at the top. In diagram B (middle), as the load reaches the critical buckling load P sub CR, the column deforms laterally into a curved shape. In diagram C (right), the free-body diagram of the column is shown for a cut taken halfway along its length, displaying the lower portion of the column. A coordinate system is included, with the x-axis vertical and the y-axis horizontal. At the base, a pin support reacts with an upward force labeled P. A dashed line represents the original central axis of the column, passing through the middle of the curved shape. At the midpoint, a downward force labeled P prime acts along this axis. The lateral deflection of the column from the x-axis at the cut is labeled y, and an internal clockwise moment labeled M is shown at the cut with a curved arrow.
Figure 15.4: Pinned-pinned axially loaded column

Columns are similar to beams rotated 90°, so we can use what we already know about the elastic curve.

\[ \frac{d^2 y}{d x^2}=\frac{M}{E I} \]

We can use the FBD in Figure 15.4 (C) to sum moments about any point on the lower column section.

\[ \begin{aligned} & \sum M=0=M+P y \\ & M=-P y \end{aligned} \]

We can now substitute this expression into the elastic curve equation.

\[ \begin{aligned} & \frac{d^2 y}{d x^2}=\frac{-P y}{E I} \\ & \frac{d^2 y}{d x^2}+\left(\frac{P}{E I}\right) y=0 \end{aligned} \]

This is a linear, homogeneous, second-order differential equation with constant coefficients, which has a general solution of

\[ y=C_1 \sin \left(\sqrt{\frac{P}{E I}} x\right)+C_2 \cos \left(\sqrt{\frac{P}{E I}} x\right) \]

The two constants, C1 and C2, can be determined by imploring boundary conditions. Since y = 0 at x = 0 and y = 0 when x = L, the first condition results in

\[ \begin{aligned} &0 =C_1(0)+C_2(1) \\ & C_2 =0 \end{aligned} \]

The second boundary condition, x = L when y = 0, results in

\[ 0=C_1 \sin \left(\sqrt{\frac{P}{E I}} x\right)+0 \]

The equation is satisfied if C1 = 0. However, this is a trivial solution that implies y = 0 and there is no lateral deflection. For the nontrivial solution, the sine function must be equal to zero, which requires

\[ \begin{aligned} &\sqrt{\frac{P}{E I}} L=n \pi \\ & \text {where } n=1, 2, 3, 4,... \end{aligned} \]

The smallest value of P occurs when n = 1; substituting this and rearranging gives us Euler’s formula

\[ \boxed{P_{c r}=\frac{\pi^2 E I}{L^2}}\text{ ,} \tag{15.1}\]

where
Pcr = Critical axial load on the column just before it buckles [N, lb]. (This load must be less than the load that would cause the stress in the column to exceed the yield stress; otherwise due to yield stress the column will fail before it buckles.)
E = Elastic modulus of the material [Pa, psi]
I = Second moment of area for the column [m4, in.4]. (If Ix and Iy differ, use the smaller value.)
L = Unsupported length of the column (pinned-pinned connection) [m, in.]

This formula is named after the Swiss mathematician, Leonhard Euler, who developed it in 1744. Other buckling modes can exist (n = 2, n = 3, n = 4, etc.) but are less commonly used because the load required for the higher modes would be large. The first three buckling loads can be seen in Figure 15.5.

Figures labeled n equals 1, n equals 2, and n equals 3 are shown side by side, illustrating the first three buckling modes of a vertical column of length L. Equal and opposite critical loads, labeled P sub CR, are applied axially downward at the top and upward at the bottom. In the n equals 1 diagram on the left, the column buckles laterally into a single curved shape, bending leftward near the midpoint. A vertical dashed line indicates the original undeformed position. In the n equals 2 diagram at the center, the column deforms into an S-shaped curve. The upper half, of length L over 2, buckles leftward, while the lower half buckles rightward. The vertical dashed line again marks the undeformed shape. In the n equals 3 diagram on the right, the column exhibits three curved segments, each of length L over 3. The top and bottom segments buckle leftward, and the middle segment buckles rightward. A vertical dashed line is again present to show the original undeformed column.
Figure 15.5: First three buckling modes

15.1.3 Buckling Direction

Columns pinned at both ends with circular or square cross-sections (equal second moments of area) can buckle in any direction. For columns with asymmetric cross-sections, buckling occurs in the plane perpendicular to the axis with the smallest second moment of area. For example, a ruler in Figure 15.2 with a rectangular cross-section buckles about its weaker axis under compression. For nonsymmetric sections, both axes should be analyzed to find the smallest second moment of area, which is then used to calculate the critical buckling load. Figure 15.6 shows buckling in wood supports.

Series of vertical wooden studs in a framed wall that have buckled inward, forming lateral deflections between their top and bottom connections. The studs are likely subjected to axial compression from the roof framing above. Several members exhibit single-curvature bowing, indicating buckling in the first mode. The studs are evenly spaced and connected at both ends but lack sufficient lateral bracing to prevent this instability.
Figure 15.6: Buckling of wooden studs

15.1.4 Critical Stress

The Euler buckling equation can be used to calculate the critical stress for a column by setting I = Ar2, where A is the cross-sectional area and r is the radius of gyration. For a more comprehensive discussion on the radius of gyration, see the Engineering Statics book by Baker and Haynes.

\[ \sigma_{c r}=\frac{P_{c r}}{A}=\frac{\pi^2 E\left(A r^2\right)}{A L^2} \]

Rearranging produces

\[ \boxed{\sigma_{c r}=\frac{\pi^2 E}{\left(\frac{L}{r}\right)^2}}\text{ ,} \tag{15.2}\]

where
σcr = Critical stress on the column just before it buckles [Pa, psi]. (This stress must be less than that of the yield stress; otherwise due to yield stress the column will fail before it buckles.)
E = Elastic modulus of the material [Pa, psi]
L = Unsupported length of the column (pinned-pinned connection) [m, in.]
r = Smallest radius of gyration of the column [m, in.]

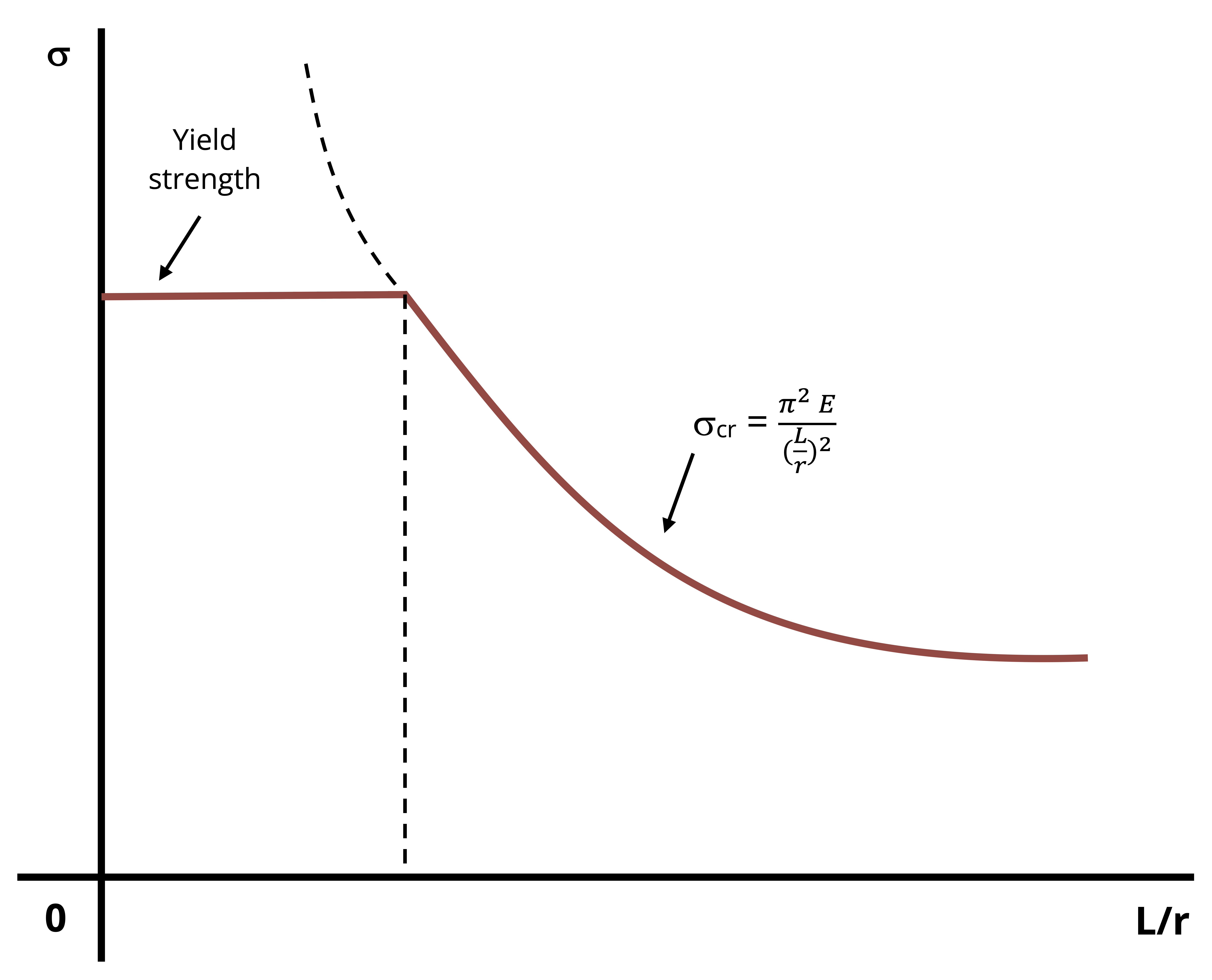
The quantity in the denominator, L/r, is called the slenderness ratio of the column. Many times this ratio is used to classify columns as short, intermediate, or long. The smallest value of the radius of gyration is used to find the critical stress.

A plot of the critical stress versus the slenderness ratio is shown in Figure 15.7. For larger slenderness ratios the curve is hyperbolic. For smaller slenderness ratios the critical stress is equal to the material’s yield stress. This graph illustrates that if the critical stress calculated using Euler’s equation is greater than the yield stress, the stress is of no interest because the column will yield before it has the chance to buckle.

Quadrant 1 of an x-y axis. Zero is in the bottom left corner. y-axis is labeled sigma. x-axis is labeled L/r. A horizontal red line juts out and then begins to form a concave upward curve. The horizontal part is labeled "yield strength" and the curved part is labeled "sigma sub cr = pi squared times E all over L/r squared."
Figure 15.7: Plot of critical stress

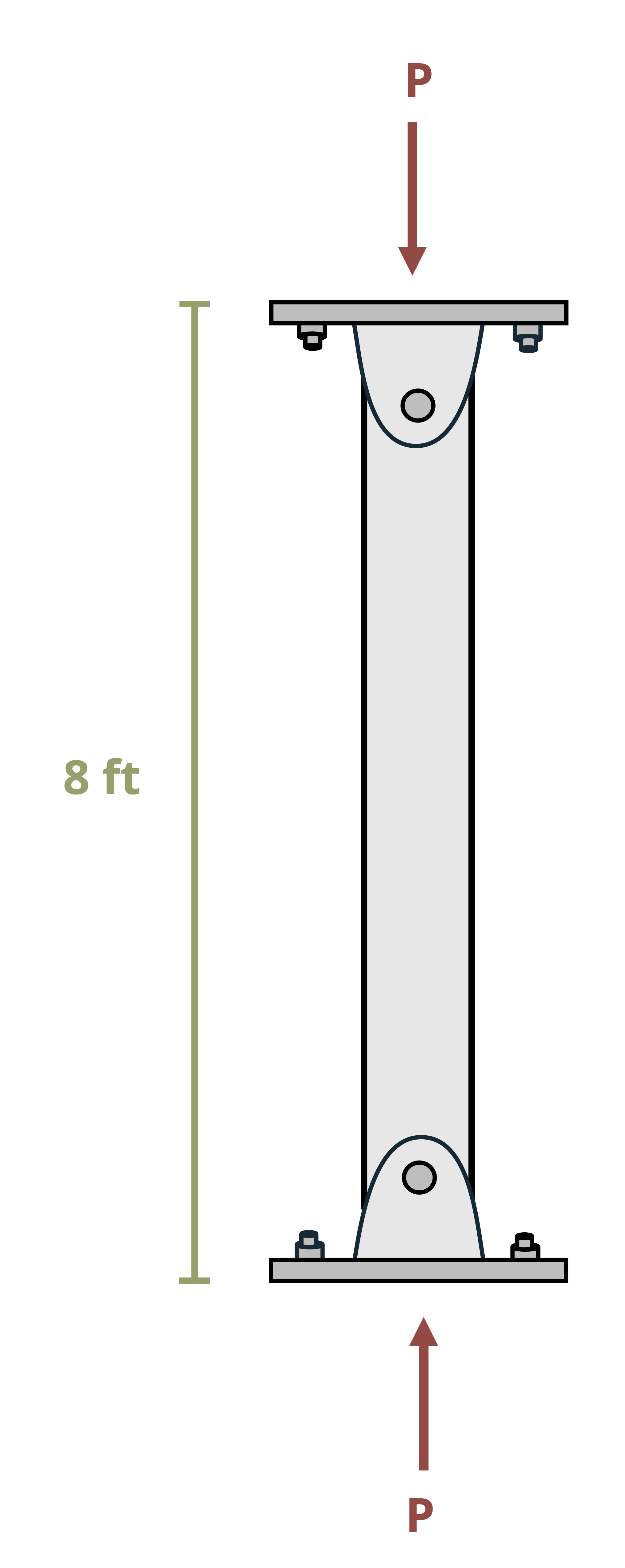
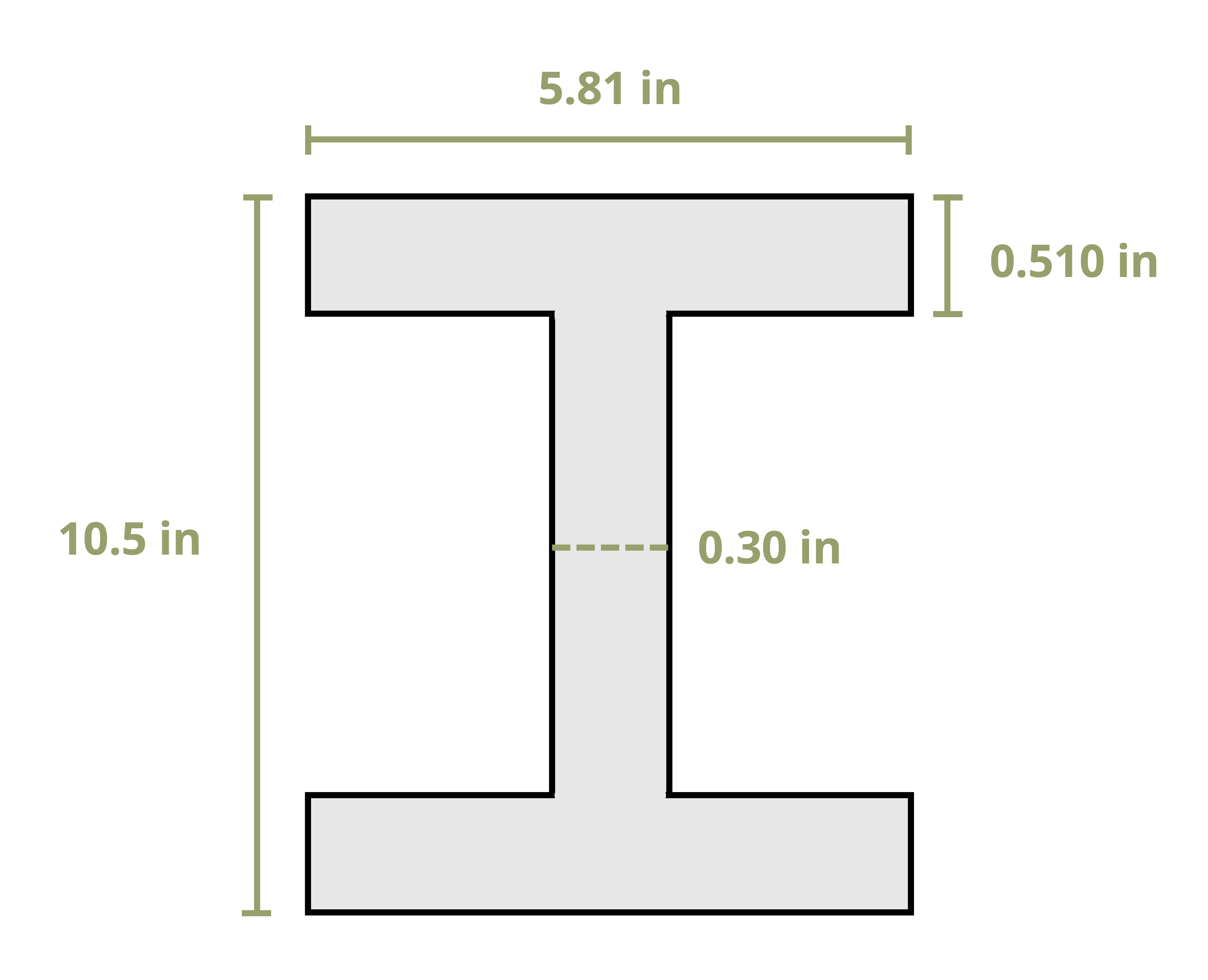
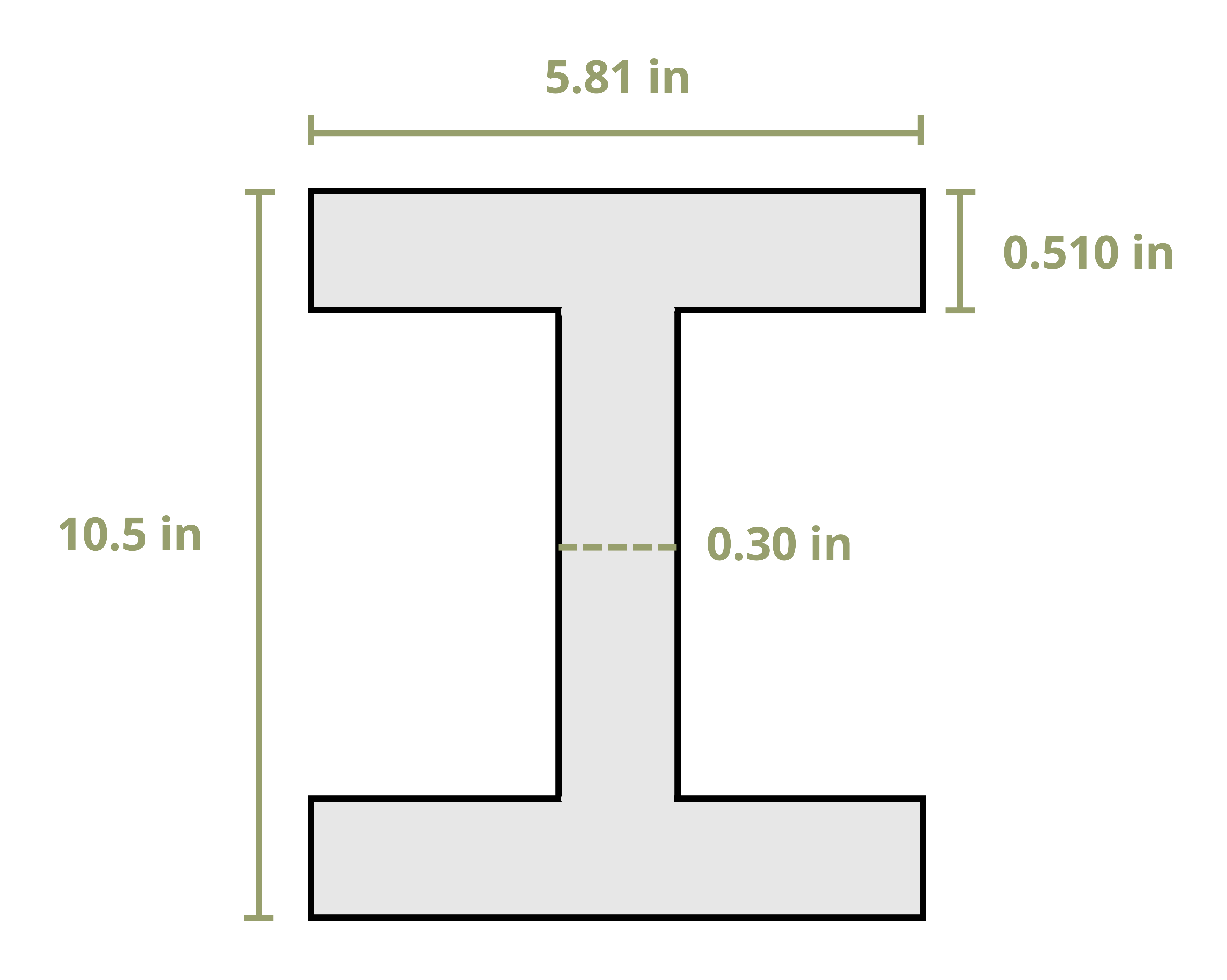
Example 15.1 demonstrates calculation of the critical buckling load and critical buckling stress.

Example 15.1  

A pinned-pinned W10 x 30 column is 8 ft long and made of A492 steel (σy = 50 ksi and E = 29,000 ksi).

What is the largest axial load this column can support?

Vertical column with pinned supports at both the top and bottom. Equal and opposite axial compressive loads labeled P are applied at each end downward at the top and upward at the bottom. The column has a total height of 8 feet measured along its length.

First consult the table in Appendix A to get the section properties of a W10 x 30 section.

Cross-sectional geometry of an I-beam with labeled dimensions: an overall height of 10.5 inches, a flange width of 5.81 inches, a flange thickness of 0.510 inches, and a web thickness of 0.30 inches.

\[ \begin{aligned} & A=8.84{~in.}^2 \\ & I_x=170{~in.}^4 \\ & r_y=4.38{~in.} \\ & I_y=16.7{~in.}^4 \\ & r_y=1.37{~in.} \end{aligned} \]

Then start by calculating the critical load using Euler’s buckling formula. Note that we can confidently say that this column will buckle about the y-axis since the second moment of area in the y direction is the smallest.

\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I}{L^2}=\frac{\pi^2(29,000{~ksi})(16.7{~in.}^4)}{\left(8{~ft}* 12\frac{in.}{ft}\right)^2} \\ & P_{cr}=518.6{~kips} \end{aligned} \]

This represents the load at which any increase in applied load will cause the column to buckle.

Next calculate the stress associated with this critical load.

\[ \sigma_{c r}=\frac{P_{cr}}{A}=\frac{518.6{~kips}}{8.84{~in.^2}}=58.7{~ksi} \]

Since this stress is larger than the yield stress of the steel (σy = 50 ksi), the column will not buckle first. It will fail due to yielding.

Calculate the force using the stress of an axial member formula discussed in Chapter 2.

\[ \begin{aligned} &\sigma_{cr} =\frac{P}{A} \\ & 50{~ksi} =\frac{P}{8.84{~in.}^2} \\ &p =442{~kips} \end{aligned} \]

WarningStep-by-Step: Buckling of Pin-Supported Columns

  1. Determine the geometric properties of the cross-section, including A, Ix, and Iy.

  2. Apply Euler’s formula to calculate the critical buckling load around the weak axis.

  3. Calculate the critical buckling stress and check that this is less than the yield stress.

  4. If the critical stress is larger than the yield stress, calculate the applied load that will cause yielding instead.

15.2 Effect of Supports

Click to expand

We derived Euler’s equation for buckling with pinned-pinned supports (the simplest case). However, in many cases columns are supported by other end conditions. Just as Euler’s formula for buckling was derived by solving a differential equation for the pinned-pinned conditions, the same can be done for other types of support cases. We will derive one more here.

Let’s consider the case where a column is fixed at one end and free at the other end as shown in Figure 15.8 (A). Summing moments at the cut end of the FBD in Figure 15.8 (B) yields M = P(δ-y).

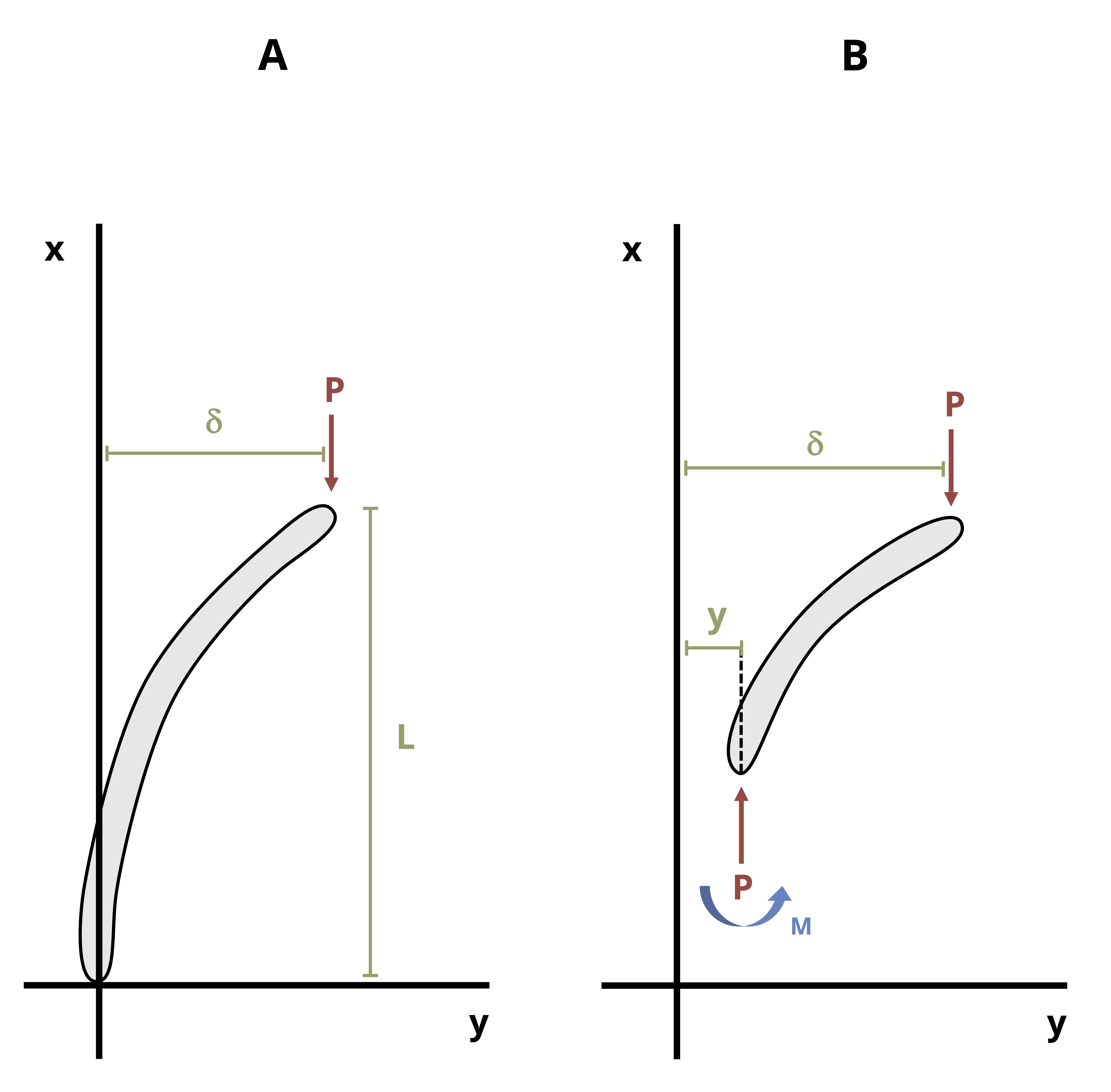
Figures labeled A and B are shown side by side, illustrating a column with a fixed base and a free end on the xy-plane, where x is the vertical axis and y is the horizontal axis. In diagram A (left), the column is fixed at the base and deflects laterally under an axial compressive load labeled P applied downward at the top. The deflected shape is parabolic, with the slope gradually decreasing from the base to the free end. The total vertical length of the column is labeled L, and the horizontal displacement at the top is labeled delta. In diagram B (right), the same deflected column is shown cut at its midpoint, with a free-body diagram of the upper portion. The axial load P continues to act downward at the top. At the cut, an internal axial force labeled P acts upward, and an internal counterclockwise moment labeled M is shown. The internal force P acts at a horizontal distance y from the x-axis, and the lateral displacement delta represents the distance between the x-axis and the line of action of the external load P.
Figure 15.8: Column with a fixed base and a free end

We can now write the differential equation using the elastic curve equation.

\[ \begin{aligned} & E I \frac{d^2 y}{d x^2}=P(\delta-y) \\ & \frac{d^2 y}{d x^2}+\left(\frac{P}{E I}\right) y=\left(\frac{P}{E I}\right) \delta \end{aligned} \]

Since the right side is not equal to zero, this equation is nonhomogeneous (note this differs from the earlier derivation for the pinned-pinned connection). There will be a particular and complementary solution.

\[ y=C_1 \sin \left(\sqrt{\frac{P}{E I} x}\right)+C_2 \cos \left(\sqrt{\frac{P}{E I} x}\right)+\delta \]

We can now employ boundary conditions to solve for the constants. At x = 0, y = 0, so C2 = δ. Also at x = 0, dy/dx = 0, so C1 = 0. This leads us to the following deflection curve:

\[ y=\delta\left(1-\cos \left(\sqrt{\frac{P}{E I}} x\right)\right) \]

At the free end of the column, x = L, we know that y = δ, and therefore

\[ 0=\delta \cos \left(\sqrt{\frac{P}{E I} L}\right) \]

The trivial solution δ = 0 shows that no matter what the P value, no buckling will occur. Thus

\[ \begin{aligned} & 0=\cos \left(\sqrt{\frac{P}{E I} L}\right) \\ & \sqrt{\frac{P}{E I}} L=\frac{n \pi}{2} \\ & \text{where n=1, 3, 5,...} \end{aligned} \]

The smallest critical load happens at n = 1 and results in

\[ P_{c r}=\frac{\pi^2 E I}{(2 L)^2} \]

Other support conditions can be derived in a similar manner.

15.2.1 Effective Length

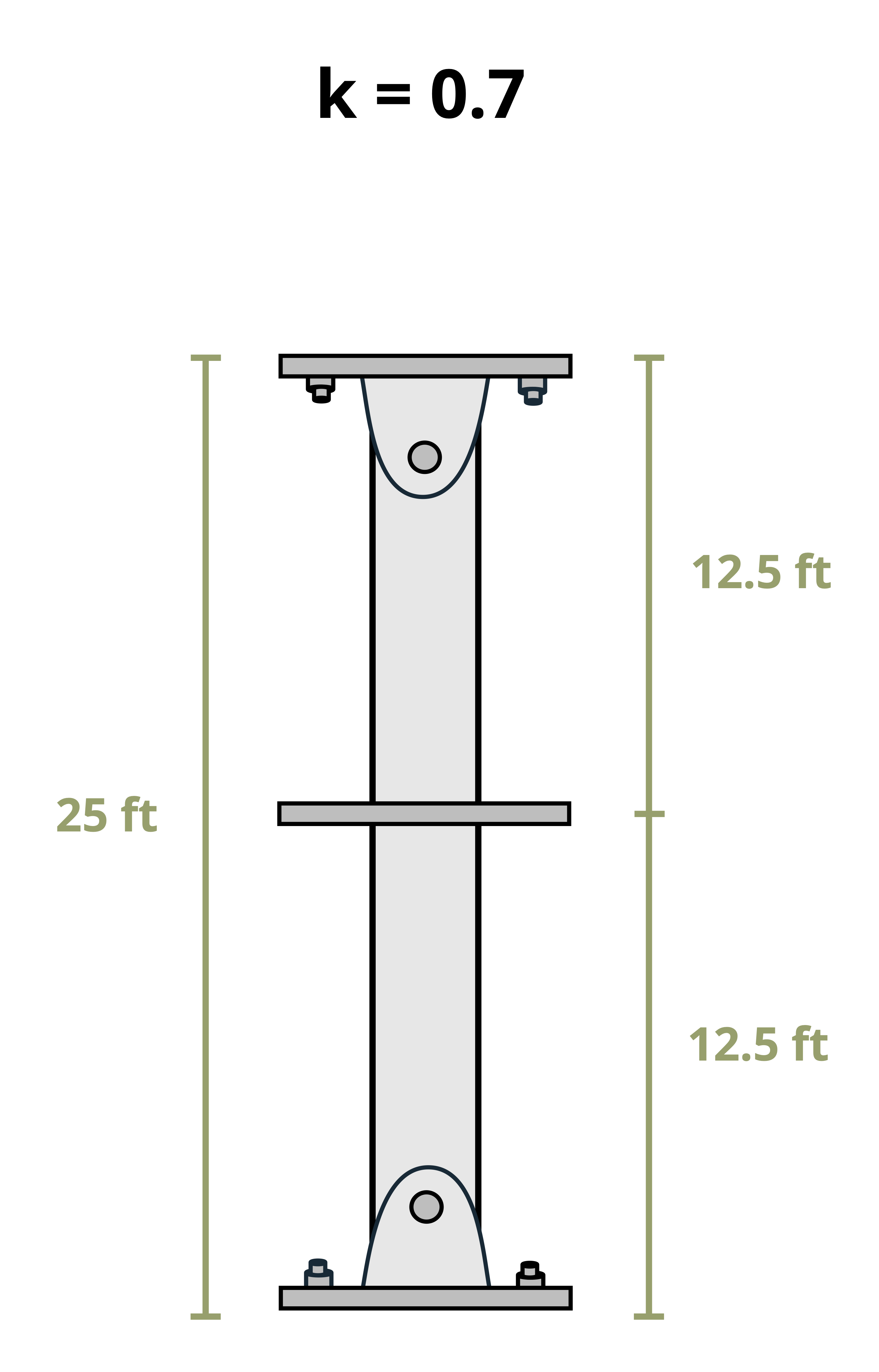
The critical load equation for a fixed-free column differs from a pinned-pinned column only by multiplying the length L by 2. The effective length, Le, is the distance between points where the moment is zero. For a pinned-pinned column, L = Le, as illustrated in Figure 15.9, whereas for a fixed-free column, Le = 2L.

Other common end conditions also relate L to Le. A general equation applies to any support condition by replacing the effective length with KL, where K is the effective length factor.

\[ \boxed{P_{c r}=\frac{\pi^2 E I}{(K L)^2}} \tag{15.3}\]

and

\[ \boxed{\sigma_{c r}=\frac{\pi^2 E}{\left(\frac{K L}{r}\right)^2}} \tag{15.4}\]

Find the effective length factor, K, below each of the end conditions in Figure 15.9.

Figures labeled k equals 1 (pinned-pinned), k equals 0.5 (fixed-fixed), k equals 0.7 (pinned-fixed), and k equals 2 (pinned-free) are shown side by side, illustrating the effective length of columns for different end conditions, each with an actual length L.In the first diagram, with k = 1, the column buckles in a smooth leftward single-curved shape, showing that the effective length L sub e is equal to L. In the second diagram, with k = 0.5, the column shows the least lateral deformation, curving leftward over a shorter single-curved region corresponding to an effective length of 0.5 times L (L sub e = 0.5 L). Portions near the top and bottom remain nearly straight due to full fixity at both ends. In the third diagram, with k = 0.7, the column bends leftward from the top pinned end while the lower fixed portion remains mostly straight. The buckled region corresponds to an effective length of 0.7 times L (L sub e = 0.7 L). In the fourth diagram, with k = 2, the pinned-free column (cantilever) exhibits the greatest lateral deflection with the effective buckling length ibeing equal to 2 times L (L sub e = 2 L). The shape begins nearly vertical at the fixed base and bends rightward, with the slope gradually decreasing toward the free end. A dashed mirrored curve is drawn on the opposite side to illustrate the corresponding full half-wave shape and to emphasize that this case exhibits the largest lateral displacement among all four end conditions.
Figure 15.9: Effective length of columns for various end conditions

Example 15.2 and Example 15.3 demonstrate how to calculate the critical buckling load in columns with various different supports.

Example 15.2  

Redo Example 15.1 with a fixed-free column.

Consult the table in Appendix A to find the section properties of a W10 x 30 section.

Cross-sectional geometry of an I-beam with labeled dimensions: an overall height of 10.5 inches, a flange width of 5.81 inches, a flange thickness of 0.510 inches, and a web thickness of 0.30 inches.

\[ \begin{aligned} & A=8.84{~in.}^2 \\ & I_x=170{~in.}^4 \\ & r_y=4.38{~in.} \\ & I_y=16.7{~in.}^4 \\ & r_y=1.37{~in.} \end{aligned} \]

Start by calculating the critical load using Euler’s buckling formula. Note that we can confidently say that this column will buckle about the y-axis since the second moment of area in the y-direction is the smallest. Use K = 2 for a fixed-free column.

\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I}{(k L)^2}=\frac{\pi^2(29,000{~ksi})(16.7{~in.^4})}{\left(2*8{~ft}*12~\frac{in.}{ft}\right)^2} \\ & P_{c r}=129.7{~kips} \\ & \end{aligned} \]

This represents the load at which any increase in applied load will cause the column to buckle.

Calculate the stress associated with this critical load.

\[ \sigma_{c r}=\frac{P_{cr}}{A}=\frac{129.7{~kips}}{8.84{~in.^2}}=14.7{~ksi} \]

Since this stress is smaller than the yield stress of the steel (σy = 50 ksi), the column will buckle first at a critical load of 129.7 kips.

Example 15.3  

A W12 x 50 column carries a load of 650 kips.

If the column is 25 ft long, has fixed-pinned end conditions, is braced at the midpoint in the weak direction, and is made from A492 steel (σy = 50 ksi and E = 29,000 ksi), is it adequate?

Vertical column with a total height of 25 feet and a lateral brace located at mid-height, dividing the column into two equal 12.5-foot segments. The column has pinned connections at both the top and bottom, and the mid-height brace provides intermediate restraint that improves buckling resistance.

\[ \begin{aligned} & A=14.6{~in.}^2 \\ & I_x=391{~in.}^4 \\ & r_y=5.18{~in.} \\ & I_y=56.3{~in.}^4 \\ & r_y=1.96{~in.} \end{aligned} \]

Cross-sectional geometry of an I-beam with labeled dimensions: an overall height of 12.2 inches, a flange width of 8.08 inches, a flange thickness of 0.64 inches, and a web thickness of 0.37 inches.

Consult the table in Appendix A to frind the section properties of a W12 x 50 section.

Start by calculating the critical load using Euler’s buckling formula. The brace at the midpoint of the column changes the length of the column in the weak direction. This doesn’t make obvious which axis the column will buckle about, so you need to check both the strong and the weak directions.

Strong axis

\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I}{(KL)^2}=\frac{\pi^2(29,000{~ksi})(391{~in.}^4)}{\left(0.7*25{~ft}*~12~\frac{in.}{ft}\right)^2} \\ & P_{c r}=2,538{~kips} \\ & \end{aligned} \]

Use the general form of Euler’s buckling equation. Since the end supports are pinned-fixed, use K = 0.7. The critical load in the strong direction is calculated to be 2,538 kips.

Compare this to buckling about the weak axis. The values of I, K, and L will change. The L value changes because the column is braced at the midpoint, so the column has a shorter distance to buckle about. The K value can be tricky, though. There were no details about the brace, so you don’t know if the brace will provide an end condition like a fixed or pinned end. So calculate the worst case, which would be a pinned-pinned end condition (this makes the denominator the largest, so the result will be the smallest).

Weak axis

\[ \begin{aligned} & P_{cr}=\frac{\pi^2 EI}{(KL)^2}=\frac{\pi^2(29,000{~ksi})(56.3{~in.^4})}{\left(1*12.5{~ft}*12\frac{in.}{ft}\right)^2} \\ & P_{c r}=716{~kips} \\ \end{aligned} \]

The critical load in the weak direction is calculated to be 716 kips. This means that if the column were to buckle, it would be about the weak axis since this load was smaller. Because the critical buckling load is greater than the 650 kip applied load, the column is adequate. However, you also need to calculate the load that would cause yielding of the steel.

Yield

\[ \begin{aligned} \sigma_{yield}=\frac{P}{4} \quad\rightarrow\quad &P=(50{~ksi})(14.6{~in.^2}) \\ & P_{yield}=730{~kips} \end{aligned} \]

Given a yielding load of 730 kips, the column is adequate for a 650 kip load. Failure would first occur by buckling in the weak direction if the load were increased to 716 kips. Note that we did not apply any safety factors. In civil engineering, design codes for steel columns designate how to apply safety factors to the loading and the capacity.

What would happen to the capacity of the columns if the brace were not there? To find out, let’s recalculate the critical load for buckling about the weak direction.

No brace

\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I}{(KL)^2}=\frac{\pi^2(29,000{~ksi})(56.3{in.^4})}{\left(0.7*25{~ft}*12~\frac{in.}{ft}\right)^2} \\ & P_{c r}=365{~kips} \\ \end{aligned} \]

Notice how much lower this is than the braced condition. If the column were not braced, it would be inadequate for the applied load.

WarningStep-by-Step: Buckling of Columns with Different Supports

  1. Determine the geometric properties of the cross-section, including A, Ix, and Iy.

  2. Determine the effective length of the column, given the supports.

  3. Apply Euler’s formula to calculate the critical buckling load. If the supports differ for each axis, calculate the critical load for both the strong and weak axes.

  4. Calculate the critical buckling stress and check that this is less than the yield stress.

  5. If the critical stress is larger than the yield stress, calculate the applied load that will cause yielding instead.

Summary

Click to expand
Note

Key Takeaways

  • Structural members that are long, slender, and subjected to compressive axial loads are categorized as columns.

  • In addition to checking stress and deflection, engineers need to check buckling as a form of member failure.

  • The critical load refers to the maximum axial load a column can withstand just before buckling occurs.

  • The effective length is the distance on the column between the points where the moment is zero. This accounts for various end conditions.

Note

Key Equations

Euler’s buckling formula (general case):

\[ P_{c r}=\frac{\pi^2 E I}{(K L)^2} \]

Critical stress formula (general case):

\[ \sigma_{c r}=\frac{\pi^2 E}{\left(\frac{K L}{r}\right)^2} \]

References

Click to expand

Figures

All figures in this chapter were created by Kindred Grey in 2025 and released under a CC BY license, except for